0.计算时间复杂度的意义
我们为什么要计算时间复杂度?
我们知道,一般来说,衡量一个代码,一般使用时间复杂度与空间复杂度。也就是说,要想写出一个接近完美的代码,你需要在时间复杂度与空间复杂度上皆优。
所以,我们计算时间复杂度,是为了计算执行当前算法所消耗的时间,从而衡量这是不是一个完美的代码。
1.时间复杂度到达多少算优?
首先,时间复杂度一般使用大O符号表示法,也就是这样: O(n) 。
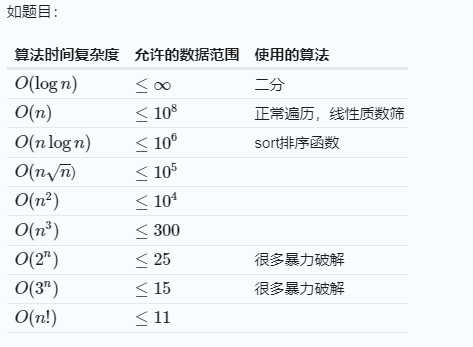
现在来看看常见的时间复杂度:
O(log n) ,也就是二分查找的复杂度。
O(n) ,遍历一遍一维数组的复杂度。
O(n log n) ,sort大法的最优复杂度。
O(n^2) ,冒泡排序的时间复杂度。
O(2^n) ,深度优先搜索的复杂度。
所以,一般来说,时间复杂度达到 O(n log n) 就非常优了,足以忍受n= 10^5~10^6 的复杂度了。
2.如何计算时间复杂度
一般来说,时间复杂度这么计算:
2.1 找出算法中的基本语句
算法中执行次数最多的那条语句就是基本语句,通常是最内层循环的循环体。
2.2 计算基本语句的执行次数的数量级
只需计算基本语句执行次数的数量级,这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可,可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析,并且使注意力集中在最重要的一点上:增长率。
2.3 用大Ο记号表示算法的时间性能
将基本语句执行次数的数量级放入大Ο记号中。