矩阵学习笔记
矩阵是线性代数中非常常用的东西,他可以用来优化,可以用来解方程,可以做很多事情。我们来看一下。
那矩阵到底是怎么被人使用的呢?那还得从方程组说起,就像下面这个方程可以表示成这样子的一个矩阵乘法的式子:
具体怎么得出来的,我们下面讲矩阵乘法时再说。
现在我们先说一下矩阵的定义:对于矩阵 A ,主对角线是指 A_{i,j} 的元素。然后一般用 I 来表示单位矩阵,也就是除了对角线是 1 ,其他位置都是 0 。
矩阵的运算
加法和减法
先说普通的加法和减法,非常简单,就是逐一元素操作,但是只有行数和列数都相同的矩形才可以进行加法和减法。
矩阵乘法
那么矩阵的乘法又是什么样子的呢?我们先搬出定义:设 A 为 P \times M 的矩阵, B 为 M \times Q 的矩阵,设矩阵 C 为 A 和 $B$ 的乘积,那么这个矩阵中的元素为:
简而言之,就是说最后结果的乘积就是前面两个矩阵分别相乘再相加得到的。至于怎么求,我们就不得不提到矩阵乘法满足的性质了,加法和减法都满足交换律和结合律,但是乘法不满足一般的交换律,所以矩阵乘法只满足结合律。所以通过结合律,我们可以使用快速幂来计算矩阵乘法。
matrix operator*(const matrix &a,const matrix &b)
{
matrix res;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
res.c[i][j]=0;
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
for(intk=1;k<=n;k++)
{
res.c[i][j]+=a.c[i][k]*b.c[k][j]%mod;
res.c[i][j]%=mod;
}
}
}
return res;
}
矩阵的逆
矩阵 A 的逆矩阵 B 是使得 A \times B = I 的矩阵。
可以使用高斯消元求解,高斯消元我们下面会讲,矩阵的逆有可能不存在。
矩阵转置
矩阵的转置,就是在矩阵的右上角写上转置 T 记号,表示将矩阵的行与列互换。
对称矩阵转置前后保持不变。
矩阵的运用
矩阵快速幂优化
不妨我们先思考一个问题,如果让你求 A^B ,你会怎么办,直接算。数据太大了。很明显,快速幂就是正解。但是,如果我让你求矩阵的幂次,怎么办呢?很明显,还是使用快速幂,那到底怎么求呢?其实方法是类似的,还是使用二进制拆分,拆分成这个样子:
因为 2 的整数次方幂可以直接计算,所以时间复杂度就变成了 O(logn) 。
matrix quick_pow(matrix a,long long kk)
{
matrix res;
for(int i=1;i<=n;i++)
{
res.c[i][i]=1;
}
while(kk)
{
if(kk&1)
res=a*res;
a=a*a;
kk>>=1;
}
return res;
}
矩阵加速递推
向上面拿到题目类似,斐波那契数列也可以使用矩阵加速,也就是说当我们要求 fib_i ,但是 i 可能会到达 10^{18} 的境界时,我们必须要使用矩阵加速递推,公式就是这个样子:
其他的话就是先构造一个矩阵,然后矩阵快速幂优化即可。
高斯消元
首先,我们先回到一开始介绍矩阵,我们需要去解一个多元一次的方程组,除了我们上面的写法,还有一种增广矩阵的做法。也就是对于形如
的矩阵,我们可以得到的增广矩阵就是:
事实上,增广矩阵其实就是把最后的和放进来,中间加了一条线就可以了。那么到底怎么做呢?首先,我们先列出一个矩阵:
然后我们就进行系数化 1 。尽量去找系数的绝对值尽可能大的。
接着系数化 1 。
然后进行相减:
然后继续重复:
最后就可以得到方程的解:
还有一种情况就是无解和无穷多种解,就是会得到未知数的系数都是 0 。然后如果得到的数不为 0 ,那么就是无解,不然就是无穷多组解。
#include<bits/stdc++.h>
using namespace std;
int n;
double a[55][55];
int cha(double w,double h)
{
return (fabs(w-h)<1e-9);
}
void solve(void)
{
int line=1;
for (int i=1;i<=n;i++)
{
int id=line;
for (int j=line+1;j<=n;j++)
if (fabs(a[j][i])>fabs(a[id][i]))
id=j;
if (cha(a[id][i],0))
continue;
swap(a[line],a[id]);
for (int j=1;j<=n;j++)
{
if (j==line)
continue;
double mul=a[j][i]/a[line][i];
for (int k=i;k<=n+1;k++)
a[j][k]-=a[line][k]*mul;
}
line++;
}
if (line<=n)
{
while (line<=n)
if (!cha(a[line++][n+1],0))
{
printf("-1");
exit(0);
}
printf("0");
exit(0);
}
}
int main(void)
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
for (int j=1;j<=n+1;j++)
scanf("%lf",a[i]+j);
solve();
for(int i=1;i<=n;i++)
{
double res=a[i][n+1]/a[i][i];
if (cha(res,0))
res=0;
printf("x%d=%.2lf\n",i,res);
}
return 0;
}
例题讲解
扑克牌
组合数学是数学的重要组成部分,是一门研究离散对象的科学,它主要研究满足一定条件的组态(也称组合模型)的存在、计数以及构造等方面的问题。组合数学的主要内容有组合计数、组合设计、组合矩阵、组合优化等。
随着计算机科学的日益发展,组合数学的重要性也日渐凸显,因为计算机科学的核心内容是使用算法处理离散数据。
今天我们来研究组合数学中的一个有趣的问题,也是一个简单的计数问题:
从一副含有 𝑛n 张的扑克牌(每张扑克牌都不相同)中,分给 m 个人,第 i 个人得到 a_i 张牌,求一共有几种分法,这个数可能非常大,请输出此数模 10007 后的结果。
这一题我认为跟矩阵的关系不大,思路就是遍历所有元素,每次从剩下的扑克牌中选若干张牌,由此可以得出中间状态为 C_{n-a_{i-1}}^{a_i} ,即从上一次选后剩余的扑克牌中选本次要求选的扑克。然后一定要注意要边选边求模。考虑到本题的数据量不大,我们可以利用杨辉三角直接构造组合数,组合数中存放的即取模后的数(否则存不下),然后在 main 函数中直接用组合数的值。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,m,a[105],i;
int left;
int ans=1;
scanf("%d%d",&n,&m);
left=n;
for (i=1;i<=m;i++)
{
scanf("%d",&a[i]);
}
for (i=1;i<=m;i++)
{
for (int j=left;j>left-a[i];j--)
{
ans=ans*j%10007;
}
for (int k=a[i];k>=2;k--)
{
while(ans%k!=0)
ans=ans+10007;
ans=ans/k%10007;
}
left=left-a[i];
}
printf("%d",ans%10007);
return 0;
}
解方程
有一个球形空间产生器能够在 n 维空间中产生一个坚硬的球体。现在,你被困在了这个 n 维球体中,你只知道球面上 n+1 个点的坐标,你需要以最快的速度确定这个 $n$ 维球体的球心坐标,以便于摧毁这个球形空间产生器。
这道题用高斯消元来做。
这道题就是已知点 i 的 n 个坐标是 a_{i,j} ,我们要找到 x_i ,使 \sum_{j=1}^{n+1}\left(a_{i,j}-x_j\right)^2=dis 。
但是我们怎么才能把它变成高斯消元的方程组呢?
我们看看怎么消掉 dis 。
因为有 n+1 个这样的式子,那我们可以相邻的两个式子相减,得到 n 个没有 dis 的式子。
那我们把平方折开,然后再减,就得到这个式子:
然后拆开 \sum_{\mathrm{j}=1}^{\mathrm{n}} 得到:
再移一下项,把 x_i 放到左边:
把左边 \sum_{\mathrm{j}=1}^{\mathrm{n}} 拆开,那我们就得到了高斯消元的矩阵。
那么接下来,我们只需要预处理高斯消元就可以轻松过了。
#include<bits/stdc++.h>
using namespace std;
double a[20][20],b[20],c[20][20];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n+1;i++)
for(int j=1;j<=n;j++)
scanf("%lf",&a[i][j]);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
c[i][j]=2*(a[i][j]-a[i+1][j]);
b[i]+=a[i][j]*a[i][j]-a[i+1][j]*a[i+1][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=i;j<=n;j++)
{
if(fabs(c[j][i]>1e-8))
{
for(int k=1;k<=n;k++)
swap(c[i][k],c[j][k]);
swap(b[i],b[j]);
}
}
for(int j=1;j<=n;j++)
{
if(i==j)
continue;
double pos=c[j][i]/c[i][i];
for(int k=i;k<=n;k++)
c[j][k]-=c[i][k]*pos;
b[j]-=b[i]*pos;
}
}
for(int i=1;i<n;i++)
printf("%0.3lf ",b[i]/c[i][i]);
printf("%.3lf\n",b[n]/c[n][n]);
return 0;
}
行列式求值
这题妥妥模版题,不说了。
杰杰的女性朋友
这道题的题目看起来十分的鬼畜,又是三元组又是什么 in 和 out 的东东,但是事实上这道题目就是求 a 到 b 的路径。由于是完全图且K固定,就可以当成是每个原图点往k个中转点连了 in_{i,k_j} 条边,每个中转点往每个原图点连 out_{k_j,i} 了条边。于是我们就可以把中途要转的点和原图直接取反一波,接着用一下矩阵快速幂就可以了。
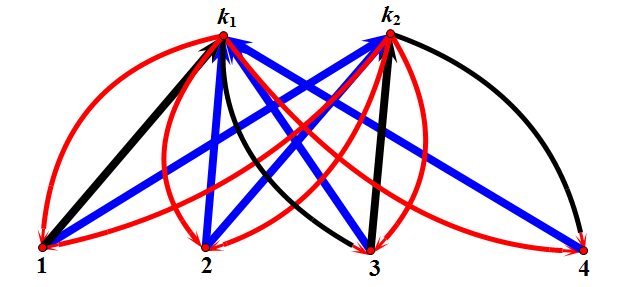
代码如下:
#include<cstdio>
#include<algorithm>
using namespace std;
#define LL unsigned long long
const int maxn=1010,maxk=25,p=1000000007;
int o[maxn][maxk],nu[maxk][maxn],jie[maxn][maxk],i1[maxk][maxn],a[maxn][maxn],
t1[maxn][maxn],t2[maxn][maxn];
int n,k;
int q,u,v,d,ans;
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=k;j++)
scanf("%d",&o[i][j]);
for(int j=1;j<=k;j++)
scanf("%d",&nu[j][i]);
}
scanf("%d",&q);
while (q--)
{
scanf("%d%d%d",&u,&v,&d);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=k;j++)
{
jie[i][j]=o[i][j];
i1[j][i]=nu[j][i];
}
}
for(int i=1;i<=n;i++)
{
jie[i][k+1]=(i==v);
i1[k+1][i]=0;
}
jie[n+1][k+1]=i1[k+1][n+1]=1;
for(int i=1;i<=k+1;i++)
{
for(int j=1;j<=k+1;j++)
{
a[i][j]=0;
for(int x=1;x<=n+1;x++)
a[i][j]=(a[i][j]+(LL)i1[i][x]*jie[x][j])%p;
}
}
for(int i=1;i<=k+1;i++)
{
for(int j=1;j<=k+1;j++)
{
t1[i][j]=a[i][j];
a[i][j]=(i==j);
}
}
while(d)
{
if(d&1)
{
for(int i=1;i<=k+1;i++)
{
for(int j=1;j<=k+1;j++)
{
t2[i][j]=0;
for(int x=1;x<=k+1;x++)
t2[i][j]=(t2[i][j]+(LL)a[i][x]*t1[x][j])%p;
}
}
for(int i=1;i<=k+1;i++)
for(int j=1;j<=k+1;j++)
a[i][j]=t2[i][j];
}
d>>=1;
for(int i=1;i<=k+1;i++)
{
for(int j=1;j<=k+1;j++)
{
t2[i][j]=0;
for(int x=1;x<=k+1;x++)
t2[i][j]=(t2[i][j]+(LL)t1[i][x]*t1[x][j])%p;
}
}
for(int i=1;i<=k+1;i++)
for(int j=1;j<=k+1;j++)
t1[i][j]=t2[i][j];
}
for(int i=1;i<=k+1;i++)
for(int j=1;j<=k+1;j++)
t1[i][j]=a[i][j];
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=k+1;j++)
{
a[i][j]=0;
for(int x=1;x<=k+1;x++)
a[i][j]=(a[i][j]+(LL)jie[i][x]*t1[x][j])%p;
}
}
ans=0;
for(int i=1;i<=k+1;i++)
ans=(ans+(LL)a[u][i]*i1[i][n+1])%p;
printf("%d\n",ans);
}
}
数路径
给你一个有 n 个顶点(编号为 1 至 $n$)和 m 条定向边的图。计算由 k 边组成的路径,并打印出以 10^9+7 为模数的答案。一条路径可以多次访问同一个顶点或边。
这道题就是模版相互堆砌,也就说这一道题就是矩阵快速幂优化配合矩阵乘法的大水题目,好的,那么只要认真看过前面的,应该都会写吧。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,k,p=1000000007;
struct matrix
{
int a[101][101];
matrix(){
memset(a,0,sizeof(a));
}
void build(){
for(int i=1;i<=n;i++){
a[i][i]=1;
}
}
}a,b,c;
matrix operator *(const matrix &x,const matrix &y)
{
matrix z;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
z.a[j][k]+=x.a[j][i]*y.a[i][k]%p;
z.a[j][k]%=p;
}
}
}
return z;
}
matrix mtqmi(matrix a,int x)
{
matrix ret;
ret.build();
while(x)
{
if(x&1)
{
ret=ret*a;
}
a=a*a;
x>>=1;
}
return ret;
}
signed main()
{
cin>>n>>m>>k;
for(int i=1;i<=m;i++)
{
int t1,t2;
cin>>t1>>t2;
a.a[t1][t2]=1;
}
a=mtqmi(a,k);
int ans=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
ans+=a.a[i][j];
ans%=p;
}
}
cout<<ans;
return 0;
}
