难题,膜拜出题人
题目翻译
给定 n 个二次函数,第 i 个二次函数形如 f(x) = a_i x^2 + b_i x + c_i (其中 x 取值范围为整数 , 保证 0 < a_i \le 10^8 , -10^8 \le b_i, c_i \le 10^8 )
求前 m 小的函数值并输出
解题思路
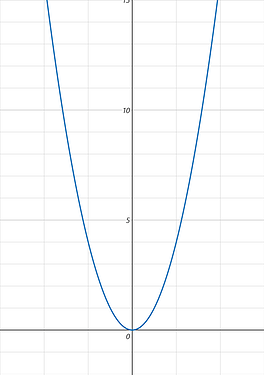
我们知道二次函数基本长这样(其二次项系数大于 0 )
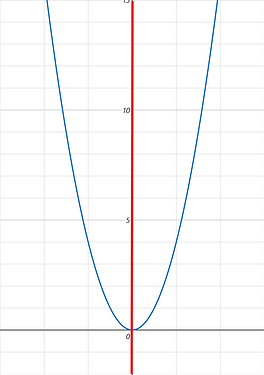
很明显,它有一个对称轴
我们要找的就是弧线上的点 x 所求出的二次函数的值
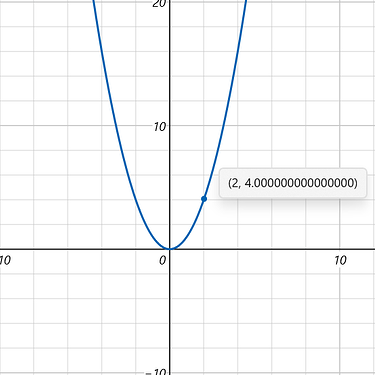
它可以在对称轴右边
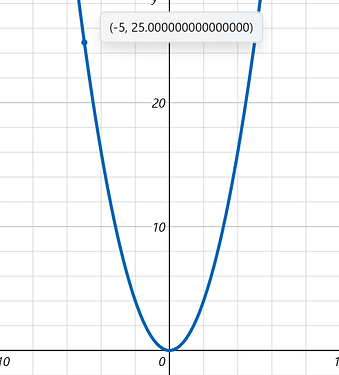
它也可以在对称轴左边
在所有在弧线上的点 x 所求出的二次函数的值中,在对称轴上的 f(x) 值是最小的
设 x' 且为函数 f(x) 在对称轴上的 x 的值
则很容易就能想到
f(\lceil x' \rceil) 和 f(\lfloor x' \rfloor) 一定是所有 f(x) 中的最小值和次小值
所以我们有了这样一个思路
a.遍历每个二次函数,对于第 i 个函数,求出 f_i(\lceil x' \rceil) 和 f_i(\lfloor x' \rfloor) 并存入优先队列
b.循环 m 次
\hspace{0.5cm} 1.输出堆顶元素
\hspace{0.5cm} 2.扩展堆顶元素*
[扩展堆顶元素]:此处的扩展堆顶元素指
\hspace{0.5cm} 1.若 x_{top} < x' 且此时堆顶为第 i 个二次函数则将 f_i(x_{top}-1) 存入优先队列
\hspace{0.5cm} 2.若 x_{top} > x' 且此时堆顶为第 i 个二次函数则将 f_i(x_{top}+1) 存入优先队列
玄学
代码
结构体定义
struct node2//优先队列结构体
{
int x, y, z, now, num;//x,y,z表示构成这个二次函数的三个要素,num表示这个二次函数的值,now表示现在x时多少
bool b;//b表示这个函数该往哪个方向扩展
};
执行操作
for (int i = 1; i <= n; i++)//执行 a 操作
{
int x = (-a[i].y) / (a[i].x * 2);
int ux = x +1, dx = x;
q.push((node2){a[i].x, a[i].y, a[i].z, ux, a[i].x * ux * ux + a[i].y * ux + a[i].z, 0});
q.push((node2){a[i].x, a[i].y, a[i].z, dx, a[i].x * dx * dx + a[i].y * dx + a[i].z, 1});
}
for (int i = 1; i <= m; i++)//执行 b 操作
{
node2 x = q.top();
q.pop();
printf("%lld ", x.num);
if (x.b)
{
int dx = x.now - 1;
q.push((node2){x.x, x.y, x.z, dx, x.x * dx * dx + x.y * dx + x.z, 1});
}
else
{
int ux = x.now + 1;
q.push((node2){x.x, x.y, x.z, ux, x.x * ux * ux + x.y * ux + x.z, 0});
}
}