{\color{Orange} {\Huge 图} }
学习杨晋华 : {\color{Green} {\Huge 还是LaTeX大佬} } @杨晋华
1. 存图方式
存图方式一般有:
邻接表,前向星,vector等
邻接表
struct Arc {
//每条边在对应在顶表中的位置
int arc_pos;
//边的权重
int arc_weight;
//边的下一个节点指针
Arc* arc_next;
};
//顶点表
struct Ver {
//顶点的编号(这里就式顶点数组的下表了)
int ver_name;
//顶点中指向第一个节点的指针
Arc* ver_next;
//顶点是否访问过
bool ver_viste = false;
};
前向星
// (u, v, w): 有一条边,从u节点指向v节点,权重为w
// 在每一次添加边时,cnt都表示当前未分配的边的编号,添加边后cnt需++
void addEdge(int u, int v, int w) {
next[cnt] = head[u];
to[cnt] = v;
weight[cnt] = w;
head[u] = cnt;
++cnt;
}
vector
vector<pair<int, int>> mp[5005];//建vector
int main()
{
int n, m;//一个N*M的图
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int x, y, w;
cin >> x >> y >> w;
mp[x].push_back({y, w});//push_back进去
}
}
2. 图的类型
图分为两种:
图和树,接下来就盘点一下图的不同种类吧 ![]()
先是我喜欢的树开始
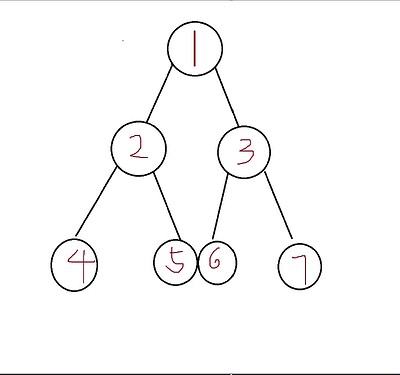
第一种 ~那必须是二叉树啊~
这个是完全二叉树(图画的丑,勿喷)
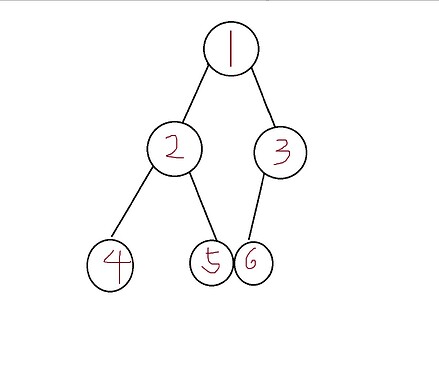
这个是不完全二叉树
不完全二叉树
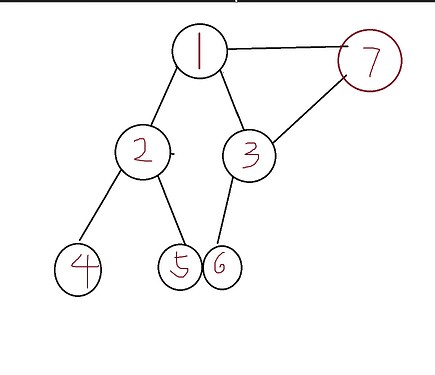
这个是基环树,顾名思义就是支友一个环的树
另外还有没有右子树和没有左子树的二叉树,这里我就不展开了
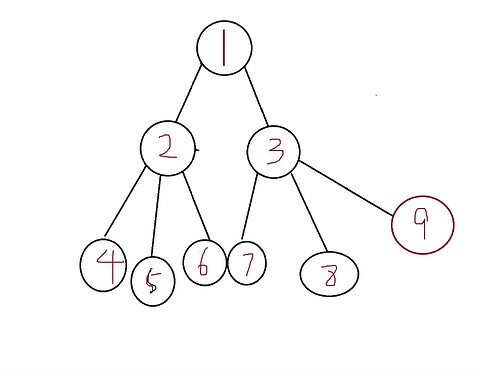
第2种树
不二叉的树(废话)
这种树一般不怎么好存,所以我叫它司(hao)母(yong)树顶(非常司(hao)母(yong)的树)
接下来就是庞大的图家族了
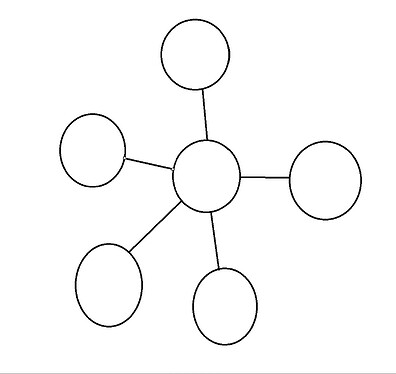
第一种
无向无环图(我画的这个也叫菊花图)
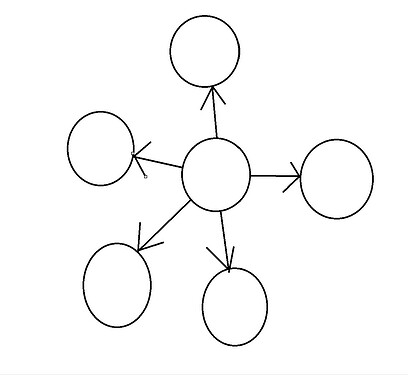
有向无环图
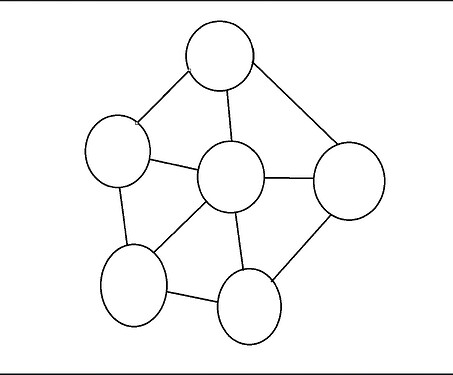
无向有环图
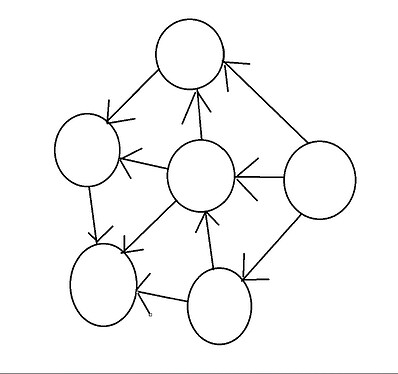
有向有环图
常用的树和图基本就是这些了(如果有我没有写的记得提醒我哦)
3. 关于图的基本算法
基本的算法大家最熟悉的就是DFS和BFS了
1.DFS
1为了求得问题的解,先选择某一种可能情况向前探索;
2在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索;
3如此反复进行,直至得到解或证明无解
Void DFS(deep,...){
if(找到解 || 走不下去了){
......//根据题意添加
return;
}
for(扩展方式){
if(扩展方式所能达到的状态合法){
修改操作;//根据题意添加
标记;
DFS(deep+1,...);
//根据题意是否要还原
}
}
}
2.BFS
BFS一般是解决一些连通块,最短路,走迷宫等的题目的
void BFS(){
初始化队列Q;
起点S入队;
标记S已经访问;
while(Q非空){
取Q的队首元素U;
U出队列;
if(u==目标状态){
返回结果;
}
for(所有与U相邻的元素){
if(相邻的元素合法 && 未访问){
入队;
标记访问;
}
}
}
}
DFS和BFS金典例题
1.
题目描述
机器猫被困在一个矩形迷宫里。
迷宫可以视为一个
n×m 矩阵,每个位置要么是空地,要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。
机器猫初始时位于
(1,1) 的位置,问能否走到
(n,m) 位置。
输入格式
第一行,两个正整数
n,m。
接下来
n 行,输入这个迷宫。每行输入一个长为
m 的字符串,# 表示墙,. 表示空地。
输出格式
仅一行,一个字符串。如果机器猫能走到
(n,m),则输出 Yes;否则输出 No。
输入输出样例
输入 #1复制
3 5
.##.#
.#...
...#.
输出 #1复制
Yes
说明/提示
样例解释
路线如下:
(1,1)→(2,1)→(3,1)→(3,2)→(3,3)→(2,3)→(2,4)→(2,5)→(3,5)
数据规模与约定
对于 100% 的数据,保证 1≤n,m≤100,且 (1,1) 和(n,m) 均为空地。
dfs 的方法就是找一条路走,直到碰壁后换一条走。
还有一种方法,我们可以逐层展开搜索:
搜索一步能到达的点;
搜索两步能到达的点;
搜索三步能到达的点;
这种方法我们成为广度优先搜索(宽度优先搜索,bfs)。
使用广度优先搜索就要使用到队列,存储待访问的点。
AC代码(我自己的)
#include<bits/stdc++.h>
using namespace std;
int m,n;
bool vis[105][105];
char mp[105][105];
int px[] = {0,0,1,-1};
int py[] = {1,-1,0,0};
void fun(int x,int y)
{
if(x < 1 || x > n||y > m||y < 1 ||vis[x][y] == 1 || mp[x][y] == '#')
{
return;
}
vis[x][y] = 1;
for(int i = 0;i <= 3;i++)
{
int cx = x + px[i];
int cy = y + py[i];
fun(cx,cy);
}
}
int main()
{
cin>>n>>m;
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
cin>>mp[i][j];
}
}
fun(1,1);
if(vis[n][m] == 1)
{
cout<<"Yes";
}
else
{
cout<<"No";
}
return 0;
}
2
# 填涂颜色
## 题目描述
由数字 $0$ 组成的方阵中,有一任意形状的由数字 $1$ 构成的闭合圈。现要求把闭合圈内的所有空间都填写成 $2$。例如:$6\times 6$ 的方阵($n=6$),涂色前和涂色后的方阵如下:
如果从某个 $0$ 出发,只向上下左右 $4$ 个方向移动且仅经过其他 $0$ 的情况下,无法到达方阵的边界,就认为这个 $0$ **在闭合圈内**。闭合圈不一定是环形的,可以是任意形状,但保证**闭合圈内**的 $0$ 是连通的(两两之间可以相互到达)。
```plain
0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 1 0 1
1 1 1 1 1 1
0 0 0 0 0 0
0 0 0 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 1 2 1
1 1 1 1 1 1
输入格式
每组测试数据第一行一个整数 $n(1 \le n \le 30)$。
接下来 n 行,由 0 和 1 组成的 n \times n 的方阵。
方阵内只有一个闭合圈,圈内至少有一个 $0$。
输出格式
已经填好数字 2 的完整方阵。
样例 #1
样例输入 #1
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
样例输出 #1
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
提示
对于 100\% 的数据,$1 \le n \le 30 $ 。
这题就是BFS了
我就是先把找到的位置染上色然后输出的时候按照颜色输出就好了
AC
#include<bits/stdc++.h>
using namespace std;
int n,m,ans;
int mp[105][105];
int x[] = {-1,1,0,0};
int y[] = {0,0,-1,1};
void dfs(int a,int b)
{
for(int i = 0;i < 4;i++)
{
int cx = a + x[i],cy = b + y[i];
if(cx > n + 1 || cx < 0|| cy > n + 1 || cy < 0 ||mp[cx][cy] == 1||mp[cx][cy] == 2)
{
continue;
}
mp[cx][cy] = 2;
dfs(cx,cy);
}
}
int main()
{
cin>>n;
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= n;j++)
{
cin>>mp[i][j];
}
}
dfs(0,0);
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= n;j++)
{
if(mp[i][j] == 2)
{
cout<<0<<" ";
}
else if(mp[i][j] == 0)
{
cout<<2<<" ";
}
else
{
cout<<1<<" ";
}
}
cout<<'\n';
}
return 0;
}
{\color{Orange} {\Huge 最后,制作不易,点赞。} }