动态规划背包总结
背包是dp的一个延伸,一般是一组东西,给定重量与价值,使其在某一个重量范围内获得最多的价值。
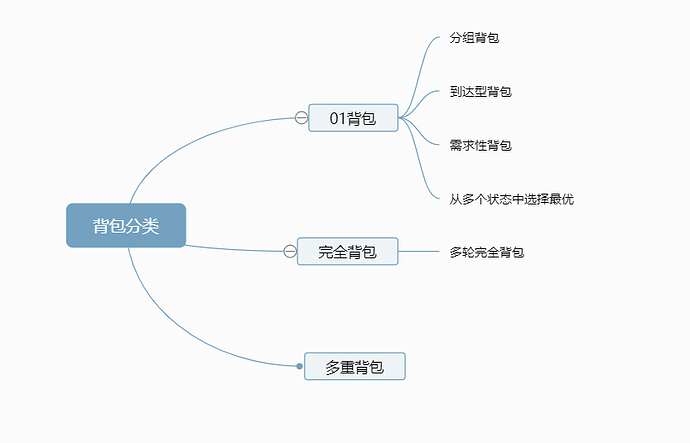
首先上一副背包的大致分类总结图
- 01背包
- 01背包延伸
- 完全背包
- 多重背包
一、01背包
解释
模板题
给定一个最大承重为 W 的背包,n 个物品,第 i 个物品重量为 w[i],价值为v[i]。
问:在不超过背包最大承重的情况下,能取得的最大总价值为多少?
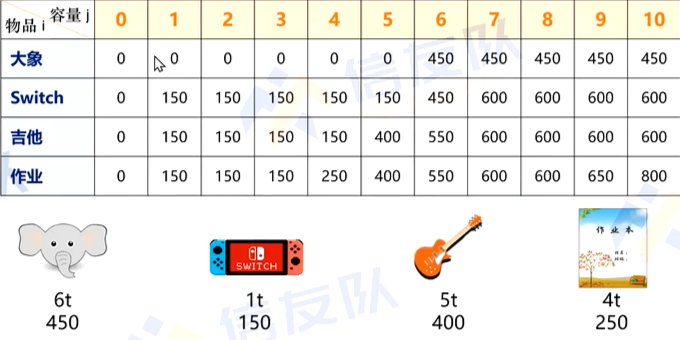
这个问题让我们首先想到的就是暴力枚举,可是复杂度十分的可观,所以,我们就可以使用我们的dp,从而减少复杂度。所以我们可以得到这样一张图。
’
在这里,我们运用一个定长二维数组存下,在用1~i这几个物品背包j的容量时能存下最多价值的物品。
所以就可以得出状态转移公式dp[j]=max(dp[j],dp[j-w[i]]+c[i]);
二、01背包延伸
除了普通的01背包,01背包还有一些延伸,也十分的重要
分组背包:
每组那还是不拿(拿哪个?)01的对象,具备多个形态,我们需要取最优。
到达型背包:
一般会带有《恰好》这样的字眼,对状态转移公式做了严格限制。
需求性背包:
转移条件一般很宽松,但是要考虑剩余需求为0时的情况
三、完全背包
模板题
给定一个最大承重为 𝑊的背包,𝑛种物品,第𝑖种物品重量为 𝑤𝑖,价值为 𝑣𝑖。
每种物品都有无限个。
问:在不超过背包最大承重的情况下,能取得的最大总价值为多少?
将第 i 种物品塞入背包的代码:
正序转移
for (int j = w[i];j <= W;j++)
f[j] = max(f[j], f[j-w[i]] + v[i]);
时间复杂度:𝑂(𝑛×𝑊)
四、多重背包
模板题
给定一个最大承重为 𝑊的背包,𝑛种物品,第𝑖种物品重量为 𝑤𝑖 ,价值为 𝑣𝑖 。第 i 种物品有 𝑚𝑖个
问:在不超过背包最大承重的情况下,能取得的最大总价值为多少?
一个简单的思路:
每种物品拆分成 𝑚𝑖个,然后对每一个物品做01背包即可。时间复杂度 𝑂(𝑊⋅∑𝑚𝑖)
可是复杂度太高了!
如何优化呢?
多重背包二进制拆分
某个物品有 𝑚𝑖个,则将其拆分为 1,2,4,…,2𝑘,𝑚𝑖−(1+2+4+8+…+2𝑘),一共 ⌈log𝑚𝑖⌉个 01 背包。
易知这样的拆分可以拼出 0∼𝑚𝑖中任意一个数量。而 01 背包可以选出最优解。所以这样做是正确的。
这就是目前的背包总结,本人才疏学浅,无法总结到位,望大家多多指教。