数学总结
一.三角函数,对数函数
略略带过了一下三角函数和对数,对数简单来说就是在 2^3=8 中求3那里的数,三角函数是有 \sin,\cos,\tan 这几个基础函数,用来求一些角的角度。
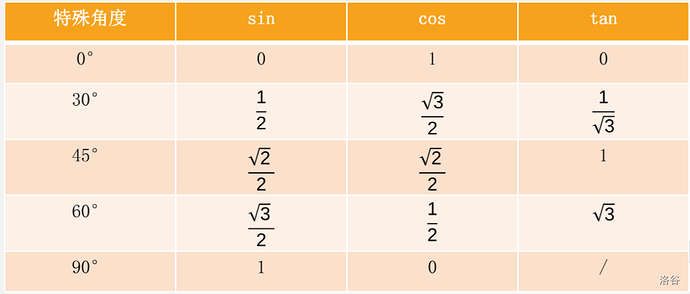
一些特殊角度的三角函数值
二.数学逻辑
然后就是数学逻辑的一些知识。
a.逻辑与:记为 \wedge ,当两个命题全部为真时,整个表达式为真。
b.逻辑或:记为 \vee ,当两个命题全部为假时,整个表达式为假。
c.逻辑非:记为 \neg ,直接否定这个命题。
d.逻辑蕴含:记为 \rightarrow 若前提为真,则结论为真。
三.集合
1.概念
集合,简称集,是数学中一个基本概念,也是集合论的主要研究对象。集合论的基本理论创立于19世纪,关于集合的最简单的说法就是在朴素集合论(最原始的集合论)中的定义,即集合是“确定的一堆东西”,集合里的“东西”则称为元素。现代的集合一般被定义为:由一个或多个确定的元素所构成的整体 。
2.集合的一些操作
a.并集
集合 A 与集合 B 的交集,记为 A \cup B ,意为将集合 A 与集合 B 中所有的元素合并在一起,合并之后将重复的数字只留下一个(去重)。
b.交集
集合 A 与集合 B 的交集,记为 A \cap B ,意为集合 A 与集合 B 中都有的元素。
用数学名词叙述为:
在集合 A 与集合 B 中,有一集合 x \in A \cup B 且 x 中所有元素都是 A 与 B 共有的,这时我们称集合 x 为集合 A 与集合 B 的交集。
四.流程图
(…流程图太难搞了,没法用latex搞,只能手画然后放图片自己画的太lj了,还是略掉吧,希望老师理解)
五.同余定理
定义
数论中的重要概念。给定一个正整数,如果两个整数 a 和 b 满足 a-b 能够被 m 整除,即 (a-b) \operatorname{mod} m=0 ,那么就称 a 与 b 对模 m 同余,记作 a\equiv b(\operatorname{mod} m) 。对模 m 同余是整数的一个等价关系。数学上,两个整数除以同一个整数,若得相同余数,则二整数同余。
同余符号
两个整数 a , b 若它们除以整数 m 的余数相等,则称 a 与 b 对于模 m 同余,或 a 同余于 b 模 m 。
记作: a\equiv b(\operatorname{mod} m)
读作: a 同余于 b 模 m ,或读作 a 同余于 b 模 m 。
证明
充分性
设a=mq1+r1,b=mq2+r2,0\le r1,r2<m
\because m \mid (a-b),a-b=m(q1-q2)+r1-r2
则有m \mid (r1-r2)
\because 0 \le r1,r2 < m
\therefore 0 \le \left | r1-r2 \right | < m
又\because m \mid (r1-r2)
即r1-r2=0
\therefore r1=r2
性质
-
反身性: a \equiv a(\operatorname{mod} m)
-
对称性:若 a \equiv b(\operatorname{mod} m) ,则 b \equiv a(\operatorname{mod} m)
-
传递性:若 a \equiv b(\operatorname{mod} m) , b \equiv c(\operatorname{mod} m) ,则 a \equiv c(\operatorname{mod} m)
-
同余式相加:若 a \equiv b(\operatorname{mod} m) , c \equiv d(\operatorname{mod} m) ,则 ac \equiv bd(\operatorname{mod} m)
-
同余式相乘:若 a \equiv b(\operatorname{mod} m) , c \equiv d(\operatorname{mod} m) ,则 ac \equiv bd(\operatorname{mod} m) (与相加相同)
运算
-
线性运算:如果 a \equiv b(\operatorname{mod} m) , c \equiv d(\operatorname{mod} m) ,那么
(1) a \pm c \equiv b \pm d(\operatorname{mod} m)
(2) a \times c \equiv b \times d(\operatorname{mod} m) -
除法:若 ac \equiv bc(\operatorname{mod} m) , c \ne 0 则 a \equiv b(\operatorname{mod} {m \div \gcd(c,m)}) ,其中 \gcd(c,m) 的意思是 c 与 m 的最大公约数,特殊地,如果 \gcd(c,m)=1 ,则 a \equiv b(\operatorname{mod} m)
-
幂运算:如果 a \equiv b(\operatorname{mod} m) ,那么 a^n \equiv b^n (\operatorname{mod} m)
乘法在性质第5条里写了,这里不再赘述。
六.排列组合
概念
排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
公式
排列: A_{r}^{n} = \frac{n!}{(r-n)!}=n \times (n-1) \times \cdots \times (n-m+1)
例: A_{6}^{5}=6 \times 5=30
组合: C_{r}^{n}=\frac{A_{r}^{n}}{A_{n}^{n}}
例: C_{8}^{3}=\frac{A_{8}^{3}}{A_{3}^{3}}=\frac{8 \times 7 \times 6}{3 \times 2 \times 1}
以上就是我的总结了,自己感觉写的还好,如果哪里有错请提出,我会非常感谢您的提议的。
Latex部分写的有点多,可能有的Latex写错了,读者们可以帮我找找错