三角函数基本定理看起来简单,不过应用大概很难(我也不讲)
这篇帖子主要是讲三角函数的基本定理
关于正弦( \sin ),余弦( \cos )和正切( \tan )
在文字上的表达:
( \Theta 为角度)
\sin \Theta =对边:斜边
\cos \Theta =邻边:斜边
\tan \Theta =对边:邻边
(聪明的同学也可以推出:余弦 \cot \Theta =邻边:对边)
为了方便同学们理解,我画了一张图
画的不好,不喜勿喷
( \cot 不用记,不会考)
除此之外
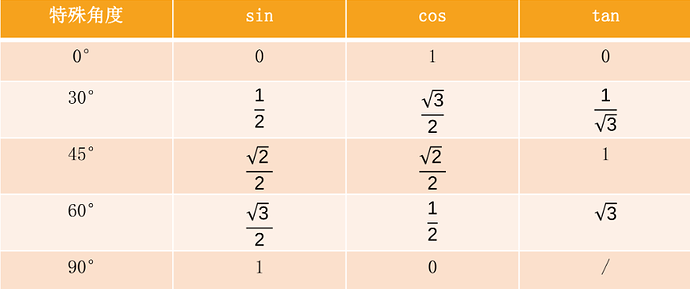
还有一些有用的公式要记
其实0°和90°的比值都不用记,也大概不会考
那么,30°,60°和90°的比值怎么记呢?
其实聪明的同学已经看出来了
\sin 和 \cos 的分母都是2
设x为1
当 \Theta =30°时 \sin \Theta = \sqrt{x} : 2
\Theta 每增长15° x+1
cos其实就是sin的倒序,这里就不过多赘述
设y= 1 : \sqrt{3}
\tan 从 y 开始
\Theta 每增长15° y * \sqrt{3}
附上一张函数图像
这个帖子做了好久,点个赞罢