7.16 初赛知识点总结

常规
1

7.16 初赛总结 智灵基础班

一、进制

计算机中除了十进制，常用的还有二进制、十六进制和八进制

在16进制中，10-15分别用A-E表示

如何表示一个数字是什么进制呢？

  • 在前面
    在前面加上0b，计算机就会认为是2进制，如0b10，就会输出2
    在前面加上一个前导0，计算机就会认为是8进制，如010，就会输出8
    在前面加上0x，即为16进制，如0x10，就会输出16
    不加任何的东西，即为10进制，如10，就会输出10
  • 在后面
    在后面加上b，代表了二进制（binary）
    在后面加上o，代表了八进制（octal）
    在后面加上d，代表了十进制（decimal）
    在后面加上h，代表了十六进制（hexadecimal）
  • 在下面
    也就是把数字写在括号内，在括号的右下角写上进制数
    例如2进制的110，可以写为
    （110）_2

这里，有一种输入方法：
在for循环中，cin一般用于cin>>a[i]，但是，还有一种方法：可以scanf("%d",a+i);这样，电脑就会获取数组a的首地址，并加上i作为偏移量，就也可以正常输入

如何把任意进制数转化回10进制数？
方法：位权
对于一个n进制数，第i位的值为第i位的位权*第i位的数值
而对于n进制数，第i位的位权为 n^{i-1} ，小数部分第j位的位权为 n^{-j}

注意：如果出现“2FH”这样的情况，那么请注意：H代表了16进制，不要以为是16！！

10进制转n进制口诀：整数部分除n取余，逆序排列；小数部分乘n取整，顺序排列

二、信息单位

在电脑里，都是用二进制存储、计算、处理和传输的
而在电脑中，常见的信息存储单位有位，字节，字等几种

  1. 位（bit）：位是计算机的最小单位，是一个二进制（一个0或1），用小写的b表示
  2. 字节（Byte）：字节是计算机的基础单位，8位代表一个字节。各种信息在电脑存储至少需要一个字节，如一个ASCII码用1个字节，一个汉字有2个字节，一个使用UTF-8编码的汉字则要使用3字节。字节用大写的B表示
  3. 字（Word）：两个字节为一个字
  4. 后面的B到KB，到MB，到GB，到TB，到PB，到EB，到ZB，到YB，到BB，下一个都是上一个的1024倍

下面是不同的数据类型在64位操作系统中的所占空间：

数据类型 在64位下的大小（字节）
bool 1
char 1
short 2
int 4
float 4
long long 8
double 8
long double 16

大家在生活之中常常会听到“32位操作系统”，“64位操作系统”的说法。那么，这两种操作系统到底有什么不同呢？
其实，这两种操作系统的不同就在于CPU一次能处理的数据量。32位的一次只能处理 2^{32}=4G 的数据，而6位的操作系统则能一次处理 2^{64} 字节的数据，即为16EB，128000000TB（1亿2800万TB）的内存

说到内存，就不得不提及关于结构体的难记的东西了

结构体内存对齐机制（怎么说的有点像游戏？）

那么，问题来了：

#include<bits/stdc++.h>
#include<windows.h>
using namespace std;
struct node{
	double a;
	int b;
	long long c;
};
int main(){
	node x={1.1,4,3};
	int y=sizeof(x);
	cout<<y;
}

你们觉得，会输出几呢？
sizeof是统计总共用了几个字节使用的
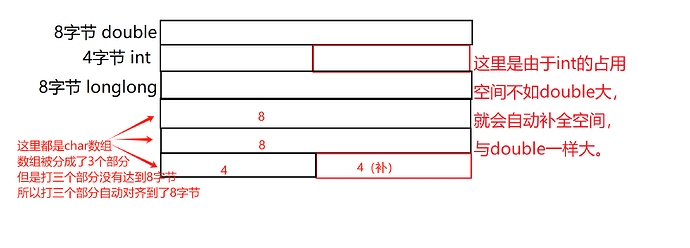
根据上表，double占用8字节，int占用4字节，longlong占用8字节，应该是20字节
那么，恭喜你，你得到了标准错误答案
正确答案是：24
具体原因请见下面截图

image
image2343×835 23.3 KB

在这里，系统为了让int类型的b与其他两个的占用空间一样大，进行了内存对齐（最大的做对齐）

#include<bits/stdc++.h>
#include<windows.h>
using namespace std;
struct node{
	double a;//8
	int b;//      4->8（内存对齐）
	long long c;//8
};
int main(){
	node x={1.1,4,3};
	int y=sizeof(x);
	cout<<y;
}

还有一个问题：

#include<bits/stdc++.h>
#include<windows.h>
using namespace std;
struct node{
	double a;
	int b;
	long long c;
        char s[20];
};
int main(){
	node x={1.1,4,3};
	int y=sizeof(x);
	cout<<y;
}

那么，会输出几呢？
你肯定会想：char类型占1字节，
而我们定义了一个20字节的数组，我们定义了4个，20 \times 4=80
那么，恭喜你又得到了标准错误答案
正确答案是：48
因为数组与变量不同，数组在内存中长这样：

image
image2471×891 111 KB

所以，最后6 \times 8，占用48字节

就是说，数组可以被拆分到不同的区域里，但是最后剩下来的那一部分还是要补全的

char定义为40呢？
这里我就不画图了
其他不变，最大为8字节
但是40能被8整除，所以，数组会被拆分为5个部分，总共8个部分，每个8字节，总共8 \times 8=64字节

三、编码形式

原码、反码、补码的基础概念和计算方法
​ 在探求为何机器要使用补码之前, 让我们先了解原码, 反码和补码的概念.对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式.

  1. 原码
    原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
    [+1]原 = 0000 0001
    [-1]原 = 1000 0001
    第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
    [1111 1111 , 0111 1111]
    即 [-127 , 127]
    原码是人脑最容易理解和计算的表示方式.

  2. 反码
    反码的表示方法是:
    正数的反码是其本身
    负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
    [+1] = [00000001]原 = [00000001]反
    [-1] = [10000001]原 = [11111110]反
    可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.

  3. 补码
    补码的表示方法是:
    正数的补码就是其本身
    负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
    [+1] = [00000001]原 = [00000001]反 = [00000001]补
    [-1] = [10000001]原 = [11111110]反 = [11111111]补
    对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.

范围解释（为什么int是从-2^31而不是-2^31+1）

详细版

以8为二进制为例：

正数的补码范围是0000 0000-0111 1111 即0-127

负数补码范围是源码1000 0000-1111 1111化为反码1111 1111-1000 0000末尾再加1，所以得到1 0000 0000-10000 0001.

1000 0001作为补码，其源码是1111 1111（-127），依次往前推，可得到-1的补码为1111 1111，那么补码0000 0000的源码是1000 0000，符号位同时也可以看做数字位即表示-128，这也解释了为什么127（0111 1111）+1（0000 0001）=-128（1000 0000）。

简单版：因为多了一个-0，所以可以访问-128

四、位运算符

位运算简介：计算机对二进制数据进行的运算都是叫位运算，即让符号位共同参与的运算。相比+-*/
这些直接使用的运算符，合理的运用位运算更能显著提高代码在机器上的执行效率。
位运算符简介：

位运算符 作用 运算规则
<< 左移 各二进制位全部左移若干位，高位丢弃，低位补0
>> 右移 各二进制位全部右移若干位，正数左补0，负数左补1，右边丢弃
& 按位与 两个位都为1时，结果才为1
按位或 按位或 两个位都为0时，结果才为0
^ 按位异或 两个位相同为0，相异为1
~ 按位取反 0变1,1变0

优先级：

优先级别 运算符
1 ~（按位取反）
2 <<（左移）、>>（右移）
3 &（按位与）
4 ^（按位异或）
5 （表格无法打出） （按位或）
6 &=、^=、（先按位或再赋值）、<<=、>>=、~=

分别解释：

  • &：
    两位同时为1，结果才为1，否则结果为0
    0101
    1100
    做&运算
    0100
    用途：
    1.清零（&0）
    2.取指定位（如取1010 1110的低4位，只要找到另一个数y，y的低四位=1，其余=0，完成与运算之后即为第四位）
    3.判断奇偶（用if((a&1)==0)来替代if(a%2==0)）

  • |：
    参加运算的只要有一个为1，其值为1
    00000011
    00000101
    做|运算
    00000111
    用途：
    1.对一个数据的某位设置为1（将x的低四位设置为1，只要与0000 1111进行或运算即可）

  • ^：
    参加运算的两个对象，如果两个数同一位相同则为0，两位不相同为1
    00000011
    00000101
    做^运算
    00000110
    用途:
    1.翻转指定位（如翻转低4位，只需要与0000 1111做异或运算，即可实现翻转）
    2.与0异或值不变
    3.交换两个数（a^=b;b^=a;a^=b;）

把位运算符与赋值运算符结合，组成&=,|=,>>=,<<=,^=等

常见的位运算符使用技巧

  1. 交换符号
int reversal(int a){
	return ~a+1;
}
  1. 求整数平均值
int average(int x,int y){
	return (x&y)+((x^y)>>1);
}
  1. 判断是否是2的幂
bool power2(int x,int y){
	return ((x&(x-1))==0)&&(x!=0);
}
  1. 求绝对值
int abs(int a){
	int i=a>>31;
	return i==0?a:(~a+1);
}
  1. 求绝对值的优化
int abs(int a){
	int i=a>>31;
	return ((a^i)-i);
}
五、ASCII码表

产生原因：
在计算机中，所有的数据在存储和运算时都要使用二进制数表示（因为计算机用高电平和低电平分别表示1和0），例如，像abcd这样的52个字母（包括大写）以及0、1等数字还有一些常用的符号（例如*#@）在计算机存储时也要用二进制数来表示，而具体哪些二进制数字表示哪个符号，当然每个人都可以自己约定自己的一套（这就叫编码），而大家如果想要互相通信而不造成混乱，那么大家就必须使用相同的编码规则，于是美国有关的标准化组织就出台了ASCII编码，统一规定了上述常用符号用那些二进制数来表示。

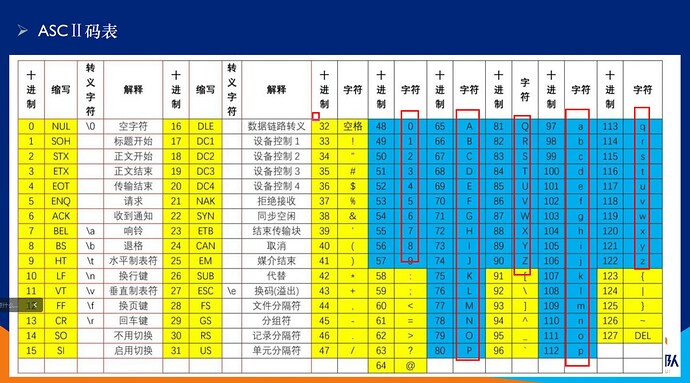
这里，我列出了常用的值：

字符 ASCII码值
空格 32
大写A 65
0 48
小写a 97

详情请看下面的对照表：

image
image1920×1066 210 KB

制作不易，点个赞吧

3 个赞