行星与王国
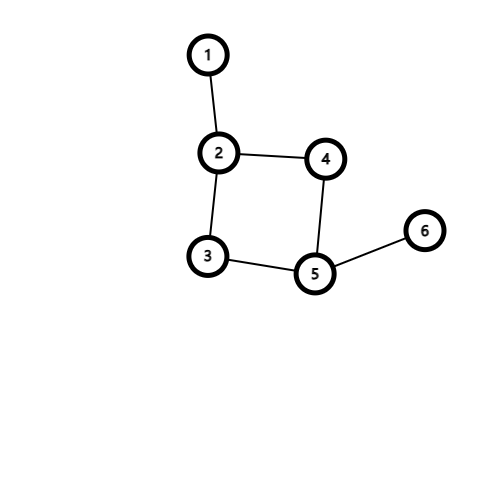
这道题目其实就是求强联通分量,上面没听懂的来看一下。好我们再次掏出一张图。
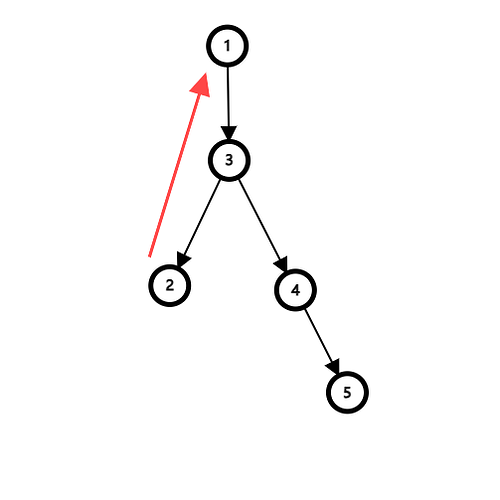
好,再来一张,不难得出下面那张图就是 dfs 生成树。然后圆圈圈出来的就是强联通分量。
再定睛一看,那一条红边就是回祖边,那么从一个点出发,一直向下遍历,然后忽得找到一个点,那个点竟然有条指回这一个点的边。说明什么,这成了一个环啦!那么,这个环上所有的点都是强联通的。
但是这只是强联通啊,我们需要求的可是强连通分量啊!QWQ
那怎么办呢?我们只需要再想一下,什么时候一个点和他的所有子孙节点中的一部分构成强连通分量?他的子孙再也没有指向他的祖先的边,却有指向他自己的边因为只要他的子孙节点有指向祖先的边,显然可以构成一个更大的强联通图。
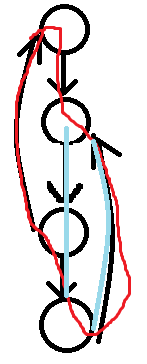
再举一个例子,红色是强联通分量,但是蓝色只是强联通图。那么我们只需要知道这个点 u 下面的所有子节点有没有连着这个点的祖先就行了。但是呢?我们怎么知道这个点u它下面的所有子节点一定是都与他强联通的呢?但是这好像有是不对的, $自己打草稿去。那怎么办呢?开个栈记录就行了。你不早说
如果在这个点之后被遍历到的点已经能与其下面的一部分点(也可能就只有他一个点)已经构成强连通分量,即它已经是最大的。那么把它们一起从栈里弹出来就行了。好了,那么代码怎么实现呢?我们只需要开这么几个数组
- dfs_i ,表示这个点在dfs时的时间戳。
- low_i ,表示这个点以及其子孙节点连的所有点中 $dfn_i$ 最小的值
- sta_i ,表示当前所有可能能构成是强连通分量的点。
- vis_i ,表示一个点是不是在栈里面。
然后再说一下 tarjan 的步骤:
- 首先初始化 dfn_u 和 low_u 第几个被 dfs 到
- 将 u 存入栈中,并将 vis_u 设为 true 。
- 遍历 u 的每一个能到的点,如果这个点 dfn 为 0 ,即仍未访问过,那么就对点 v 进行 dfs ,然后 low_u = \min (low_u,low_) 。
于是我们得到了一个强联通分量。还有一个特别的点:tarjan 一遍是搜不完所有的点的,因为存在一些孤立点,所以我们要对一趟跑下来还没有被访问到的点继续跑 tarjan 。而怎么判断呢?只需要看看 dfs 是否为 0 就好了。所以说 tarjan 的时间复杂度就是 O(n) 。至于为什么我就不多说了,好了,上代码。
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
vector<int> g[100005];
int color[100005],dfn[200020],low[200020],sta[200020],vis[100005],cnt[100005];
int deep,top,n,m,sum,ans;
void tarjan(int u)
{
dfn[u]=++deep;
low[u]=deep;
vis[u]=1;
sta[++top]=u;
int sz=g[u].size();
for(int i=0;i<sz;i++)
{
int v=g[u][i];
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else
{
if(vis[v])
{
low[u]=min(low[u],low[v]);
}
}
}
if(dfn[u]==low[u])
{
color[u]=++sum;
vis[u]=0;
while(sta[top]!=u)
{
color[sta[top]]=sum;
vis[sta[top--]]=0;
}
top--;
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int from,to;
scanf("%d%d",&from,&to);
g[from].push_back(to);
}
for(int i=1;i<=n;i++)
{
if(!dfn[i])
{
tarjan(i);
}
}
for(int i=1;i<=n;i++)
{
cnt[color[i]]++;
}
for(int i=1;i<=sum;i++)
{
if(cnt[i]>=1)
{
ans++;
}
}
printf("%d\n",ans);
for(int i=1;i<=n;i++)
{
printf("%d ",color[i]);
}
}