这是一篇关于dfs与bfs的分析:
- dfs(深度优先搜索):基本原理为使用递来模拟走一条路,一般用来求路的数量
深度优先搜索算法(depth first search, 简称dfs) 是一种用于遍历或搜索树或图的算法。沿着数的深度遍历树的节点,尽可能深的搜索树的分支。当节点v所在边都已被探寻或者在搜索时节点不满足条件, 搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有满足条件的所有节点被访问为止。
深搜,不到南墙不回头,会递归到最后面,一条一条走过去,发现没路可走了就退回去,再找,直到递归结束为止
例题1
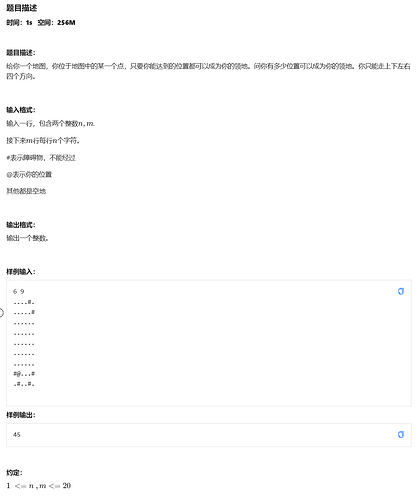
例题:领地(洪水填充问题):
样例代码(别抄):
#include<bits/stdc++.h>
using namespace std;
int n,m;
int ans=0;
char a[25][25];
bool vis[25][25];
没什么好讲的,导入定义
void f(int x,int y){//x坐标,y坐标
if(x<1||x>m||y<1||y>n||a[x][y]=='#'||vis[x][y]==1) return;//判断当前位置是否合法
vis[x][y]=1;//已被填充
ans++;//可以到的位置+1
f(x+1,y);//遍历四个边上
f(x,y+1);
f(x-1,y);
f(x,y-1);
}
上面是递归函数
int main(){
memset(vis,false,sizeof(vis));
cin>>n>>m;
int sx,sy;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
if(a[i][j]=='@'){//判断到是起点,记录起点坐标
sx=i;
sy=j;
}
}
}
f(sx,sy);
cout<<ans;
return 0;
}
例题2
例题:经典的迷宫问题
例题代码(别抄,别抄,别抄!!!):
#include<bits/stdc++.h>
using namespace std;
int n,m;
char a[8][8];
int ans=0;
上面也是没啥哈说的
void dfs(int x,int y){//x,y坐标
if(x<1||x>n||y<1||y>m||a[x][y]=='#') return;//判断如果当前点不合法,那么终止当前位置的操作
if(x==n&&y==m){//抵达目标地点,方法++
ans++;
return;
}
a[x][y]='#';//标记当前位置为无法行走,防止下面的子树走回来
dfs(x-1,y);//四个方向的递归
dfs(x+1,y);
dfs(x,y+1);
dfs(x,y-1);
a[x][y]='.';//还原当前点的位置,让其他路径能经过当前点
}
上面是最核心的电风扇哦不是dfs函数
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
dfs(1,1);//从(1,1)开始递归
cout<<ans;
return 0;
}
注意:根据题意,是从(1,1)开始的,其他题目可能与本题不同,请勿抄袭!
- bfs(广度优先搜索):基本原理为使用队列(queue)实现伪同步的效果,一般用来求最短路径
宽度优先搜索算法(又称广度优先搜索) 是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
广搜的特点是用空间换时间与深搜不同的是,广搜是用一个队列来实现伪同步的效果就是从队头取出一个元素,将取出的这个点的旁边元素遍历一遍,确认合法后把新的点放到队列最后面,以此循环往复,直到队列为空为止
例题1
这题是一题马的遍历,即马从 [sx,sy] 到 [ex,ey] 要至少几步
样例代码(别抄别抄别抄!!!!!!):
#include<bits/stdc++.h>
using namespace std;
const int fangxiangshu=8;//把这个数改成方向数
bool vis[505][505];
int n;
int sx,sy;
int ex,ey;
int dx[fangxiangshu]={-1,-2,-2,-1,1,2,2,1};//方向数组1
int dy[fangxiangshu]={-2,-1,1,2,2,1,-1,-2};//方向数组2
struct node{//节点记录结构体
int x,y,step;
};
queue<node> q;//创建一个node类型的队列
int bfs(){
q.push(node{sx,sy,0});//1.队首元素入队
while(!q.empty()){//2.遍历队列,直到队列为空
node f=q.front();//2.1 找到队首元素
q.pop();//2.2存下队首元素后,队首元素出队
for(int i=0;i<fangxiangshu;i++){//2.3遍历队首元素能到达的所有节点
int nx=f.x+dx[i];
int ny=f.y+dy[i];
if(nx==ex&&ny==ey) return f.step+1;//2.4如果当前节点是答案,return结果
if(nx>=0&&nx<n&&ny>=0&&ny<n&&!vis[nx][ny]){//2.5判断合法合法性
//2.6入队
vis[nx][ny]=1;//2.6.1 标记
q.push(node{nx,ny,f.step+1});//2.6.2 入队
}
}
}
return -1;//3 无答案
}
int main(){
cin>>n;
cin>>sx>>sy>>ex>>ey;
cout<<bfs();
return 0;
}