题目描述
小埋最近在学习有向图的遍历相关知识,小埋学习过图的遍历的相关方法,可以使用dfs或者bfs来遍历整个有向图,但是小埋发现这个问题有一些不一样,这个图的遍历是问你当前点能够到达的点的最大编号,小埋希望你能帮她解决这个问题。
输入格式
第一行两个整数一个n一个m,n代表有向图中有n个点,m代表有向图中有m条有向边。接下来是m条边。
输出格式
输出每个点能够到达的最大编号
样例
Input 1
4 3 1 2 1 3 2 3
Output 1
3 3 3 4
样例解释
样例1解释:
对于样例1,有向图如下所示:
1 → 2
| |
v v
3
|
v
4
从1开始,可以到达的最大编号是3,从2开始,可以到达的最大编号是3,从3开始,可以到达的最大编号是3,从4开始,可以到达的最大编号是4。
数据范围
数据范围:1<=n,m<=100000
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
const int MAXN = 100001;
vector<int> adj[MAXN];
bool visited[MAXN];
int max_reachable[MAXN];
void dfs(int node, int& max_index) {
stack<int> stk;
stk.push(node);
visited[node] = true;
while (!stk.empty()) {
int curr = stk.top();
stk.pop();
for (int neighbor : adj[curr]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
stk.push(neighbor);
max_reachable[neighbor] = max(max_reachable[neighbor], max_reachable[curr]);
max_index = max(max_index, max_reachable[neighbor]);
}
}
}
}
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
}
for (int i = 1; i <= n; ++i) {
visited[i] = false;
max_reachable[i] = i;
}
for (int i = 1; i <= n; ++i) {
if (!visited[i]) {
int max_index = i;
dfs(i, max_index);
max_reachable[i] = max_index;
}
}
for (int i = 1; i <= n; ++i) {
cout << max_reachable[i] << " ";
}
cout << endl;
return 0;
}
题目描述
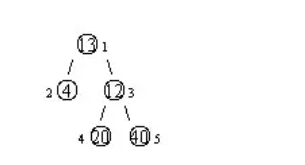
小埋最近经营n个农场,小埋要各个农场都有w个员工,每个农场也有一个编号,现在要在某个农场内建立一个物资站,使得所有员工到物资站的路程之和尽可能的小,同时约定,相邻点之间的距离为1。如上图中,若物资站建在1处,则距离和=4+12+2×20+2×40=136;若物资站建在3处,则距离和=4×2+13+20+40=81。
输入格式
第一行输入一个整数n
第二行n个数字,每个数字wi,代表每个农场的员工。
以下n-1行每行输出两个农场的编号,u,v,uv之间是双向边。
输出格式
输出一个整数,代表农场的最小距离和。
样例
Input 1
5 13 4 12 20 40 1 2 1 3 3 4 3 5
Output 1
81
样例解释
样例1解释:
物资站建在3处,距离和=4×2+13+20+40=81。
数据范围
1<=n<=100;
1<=u,v<=n;
1<=w<=1e5
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 105;
vector<int> adj[MAXN];
int w[MAXN];
int dp[MAXN][2];
void dfs(int u, int parent) {
dp[u][0] = w[u];
dp[u][1] = 0;
for (int v : adj[u]) {
if (v == parent) continue; /
dfs(v, u);
dp[u][0] += dp[v][1];
dp[u][1] += min(dp[v][0], dp[v][1]);
}
}
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> w[i];
}
for (int i = 1; i < n; ++i) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1, -1);
cout << min(dp[1][0], dp[1][1]) << endl;
return 0;
}