提高 day6 双指针 & meet in the middle整理

常规
1

双指针(two-pointer)，即同时维护两个下标或链表指针，并控制他们按一定方向移动，让整个程序枚举效率大大增加，大多数双指针部分以 O(n) 为主，是一个十分宽泛优秀的算法。

例题

例题1：

给定一个长度为 n 的严格增序列{a_n}和整数 m ，求序列中有多少对不同的数加和超过 m 。

  • 方法一：显然序列具有单调性，严格递增，题目中有写出，根据题目意思可以写出一个式子 a_i + a_j > m ，通过移项得到 a_j > m - a_i ，此时可以枚举 i ,然后根据单调性在序列中二分查找找到满足 a_j > m - a_i 的最小下标 j ,这样可以优化掉枚举 j 的那层循环，并求出合法 j 的个数，总时间复杂度为 O(n log n) ，可以通过。

  • 方法二：还是根据单调性，依然用一层循环枚举 i ，我们可以发现 a_j > m - a_i 中，最小下标 j 一定显然是随着 i 的增大，而单调不增的，所以不须二分，只需额外在维护最小 j ,让他最开始在最右边，在枚举 i 时看看 j 是否更新为更小的值即可，总时间复杂度为 O(n) ，很优秀。

例题二：

题目链接

题面： q 次询问，每次求 l ~ r 的区间和减去区间异或值得到差的最大值，若有多个最大值，去取区间长度最短的，若仍然有多个区间，输出其中一个即可，保证 q = 1, L = 1, R = n 。

大致思路：

算出 sum[i] 为前 i 个数之和， xor[i] 为前 i 个数的异或值。

  • 二分，不详讲，大致就是根据定义 f(i, j) = sum_{i,j} - xor_{i,j} ，发现对于区间 [l,r] ， f(l,r+1) ≥ f(l,r) 。
证明：

f(i, j + 1) - f(i, j)
= sum_{i, j + 1} - xor_{i, j + 1} - sum_{i, j} + xor_{i, j}

最后得出等于 ar_{j + 1} - xor_{i, j + 1} + xor_{i, j} ，证明出 f(i, j + 1) - f(i, j) ≥ 0 。

这说明了当左端点固定时，右端点向右移动时， f(i, j) 是单调不减的，具有单调性，显然二分。

代码实现
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
inline int read(){
	int r = 0,w = 1;
	char c = getchar();
	while (c < '0' || c > '9'){
		if (c == '-'){
			w = -1;
		}
		c = getchar();
	}
	while (c >= '0' && c <= '9'){
		r = (r << 3) + (r << 1) + (c ^ 48);
		c = getchar();
	}
	return r * w;
}
int n, q, ar[N], sum[N], g[N];//sum：前缀和 g：前缀异或 
int get_sum(int l, int r)
{
	return sum[r] - sum[l - 1] - (g[r] ^ g[l - 1]);//计算差值 
}
signed main()
{
	int _;
	_ = read();
	while (_ --)
	{
		n = read(), q = read();for(int i = 1;i <= n; ++ i) ar[i] = read(), sum[i] = sum[i - 1] + ar[i], g[i] = g[i - 1] ^ ar[i];
		int l = read(), r = read();
		int res = get_sum(l, r);
		int ll = l, rr = r;
		for(int i = 1;i <= r; ++ i)//枚举左端点
		{
			int Left = i, Right = r, now = 0;
			while(Left <= Right)
			{
				int mid = (Left + Right) >> 1;
				if(get_sum(i, mid) != res) Left = mid + 1;
				else Right = mid - 1, now = mid;
			}
			if(now > 0 && rr - ll + 1 > now - i + 1) ll = i, rr = now;  
		}
		cout << ll << " " << rr << "\n";
	}
	return 0;
}
  • 双指针，定义 get\_sum(l, r) 为 l ~ r 的区间和异或之差，我们可以使用尺取法， l, r 指针开始均为 1 ，枚举 l ，在定义一个 res 存最大的 get\_sum(n, n) ，如果 get\_sum(l, r) < res 且 r 没有超过 n ，那么明显 r 可以往后移动，最后再看看当前选择区间是否合法，合法即为目前最优区间。
代码实现：
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10;
inline int read(){
	int r = 0,w = 1;
	char c = getchar();
	while (c < '0' || c > '9'){
		if (c == '-'){
			w = -1;
		}
		c = getchar();
	}
	while (c >= '0' && c <= '9'){
		r = (r << 3) + (r << 1) + (c ^ 48);
		c = getchar();
	}
	return r * w;
}
int n, q, ar[N], sum[N], g[N];//sum：前缀和 g：前缀异或 
int get_sum(int l, int r)
{
	return sum[r] - sum[l - 1] - (g[r] ^ g[l - 1]);//计算差值 
}
signed main()
{
	int _;
	_ = read();
	while (_ --)
	{
		n = read(), q = read();for(int i = 1;i <= n; ++ i) ar[i] = read(), sum[i] = sum[i - 1] + ar[i], g[i] = g[i - 1] ^ ar[i];
		int l = 1, r = 1;
		int res = sum[n] - g[n];
		int ll = read(), rr = read();
		for(int i = 1;i <= n; ++ i)//枚举左端点
		{
			if(r < i) r = i;
			while(r <= n && get_sum(i, r) < res)
			{
				++ r;
			}
            if(r > n) break;
			if(rr - ll + 1 > r - i + 1) ll = i, rr = r;  
		}
		cout << ll << " " << rr << "\n";
	}
	return 0;
}

双指针拓展 floyd判环

应用于一个类似于 p 形状的图，用来找环的入口。
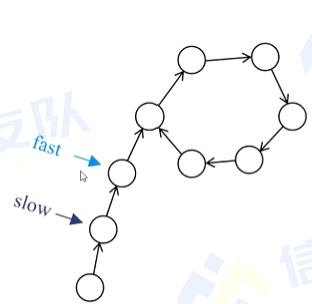
image

建立两个指针 fast, slow ，每次迭代 fast 朝着边的方向走 2 步， slow 走 1 步，知道他们走到同一个点，接着让 slow 不动， fast 回到头初始位置，然后每次迭代，两个指针都向边指向的方向移动一步，再次相遇的地方就是环的入口。

证明：

image
image860×324 67.2 KB

关于这个算法的好题（交互题）：

题目网址

大致题面：

image
image720×374 70.8 KB

大致思路：

虽然题目上写了有 10 枚棋子，但我们最多只需要用到 3 颗即可。利用类似 Floyd 判环的方法，随便拿出 2 颗棋子，其中命名慢棋子和快棋子，他们代表的意思显而易见，慢棋子移动慢，快棋子移动快。快棋子每次操作都移动一遍，慢棋子每两次操作移动一遍，那么在最多 2(t + c) 次操作后，两个棋子会相遇在一个点上，接下来每次操作把所有棋子都挪动一次，如果所有棋子都在一个点时，说明找到答案点了，总次数最多 3t + 2c 次，可以通过。

代码实现：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10;
const int MOD = 1000000007;
inline int read(){
	int r = 0,w = 1;
	char c = getchar();
	while (c < '0' || c > '9'){
		if (c == '-'){
			w = -1;
		}
		c = getchar();
	}
	while (c >= '0' && c <= '9'){
		r = (r << 3) + (r << 1) + (c ^ 48);
		c = getchar();
	}
	return r * w;
}
int n;
signed main()
{
	while(1)
	{
		cout << "next 0\n";
		fflush(stdout);
		n = read();
		for(int i = 1;i <= n; ++ i)
		{
			int x;
			x = read();
		}
		cout << "next 0 1\n";
		fflush(stdout);
		n = read();
		for(int i = 1;i <= n; ++ i)
		{
			int x;
			x = read();
		}
		if(n == 2)
		{
			break;
		}
	}
	while (1)
	{
		cout << "next 0 1 2 3 4 5 6 7 8 9\n";
		fflush(stdout);
		n = read();
		for(int i = 1;i <= n; ++ i)
		{
			int x;
			x = read();
		}
		if(n == 1)
		{
			break;
		}
	}
	cout << "done\n";
	fflush(stdout);
	return 0;
}

折半搜索(meet in the middle)，也叫中途相遇法，就是可以将搜索折半的一种方法，比如一个要计算一个搜索次数为 2^{40} 的题目，爆搜必定超时，而我们可以用类似分治的方法，把它分成一半然后计算 l, mid 和 mid + 1, r 的答案，将他们按照一定的性质结合起来。

例题一

给定 n 和一个长度为 n 的数组，有多少种方法选择一个该数组的子集使得和为 x 。

这道板子也是非常板子，就是分成两半，一半 [l,mid] ，一半 [mid + 1, r] ，每次加和完后，用 map 进行记录，最后看看存不存在计数即可。

代码实现
#include <bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){
	int r = 0,w = 1;
	char c = getchar();
	while (c < '0' || c > '9'){
		if (c == '-'){
			w = -1;
		}
		c = getchar();
	}
	while (c >= '0' && c <= '9'){
		r = (r << 3) + (r << 1) + (c ^ 48);
		c = getchar();
	}
	return r * w;
}
int n, x, a[105], res;
map <int, int> mp;
signed main()
{
	n = read();
	x = read();
	for(int i = 0;i < n;i ++) a[i] = read();
	int mid = n / 2;
	for(int i = 0;i < (1 << mid);i ++)
	{
		int s = 0;
		for(int j = 0;j < mid;j ++)
		{
			if(1 & (i >> j))
			{
				s += a[j];
			}
		}
		mp[x - s] ++;
	}
	for(int i = 0;i < (1 << (n - mid));i ++)
	{
		int s = 0;
		for(int j = 0;j < n - mid;j ++)
		{
			if(1 & (i >> j))
			{
				s += a[j + mid];
			}
		}
		if(mp.find(s) != mp.end())
		{
			res += mp[s];
		}
	}
	cout << res << "\n";
	return 0;
}

例题二

小B写了一个程序，随机生成了 n 个正整数，分别是 a_1..a_n ，他取出了其中一些数，并把它们乘起来之后模 p ，得到了余数 c 。但是没过多久，小B就忘记他选了哪些数，他想把所有可能的取数方案都找出来。你能帮他计算一下一共有多少种取数方案吗？请把最后的方案数模 1000000007 后输出。

小B记得他至少取了一个数， p 是质数。

大致思路：

首先，这个明显是折半搜索，因为暴力肯定过不了，两种状态选与不选，数总共 32 个，那么暴力搜索时间复杂度为 O(2 ^ {32}) ，显然过不了，而我们加上折半以后会发现这个题目不就是刚才那道题目，加法改成乘法了而已，注意到一个细节 p 是质数，那么说明乘法肯定要用逆元或费马小定理进行处理，再存入 map ，但这样你会发现还是 AC 不了，这是因为，你在余数在 1 的情况下，要去掉 1 的可能性，所以要减 1 ，但是 WA 90，这就要注意到一个坑点，余数不能比除数大，如果满足这个条件，肯定是没有可能性的。

代码实现：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10;
const int MOD = 1000000007;
inline int read(){
	int r = 0,w = 1;
	char c = getchar();
	while (c < '0' || c > '9'){
		if (c == '-'){
			w = -1;
		}
		c = getchar();
	}
	while (c >= '0' && c <= '9'){
		r = (r << 3) + (r << 1) + (c ^ 48);
		c = getchar();
	}
	return r * w;
}
int fast_pow(int a,int b,int p){
	int res = 1;
	while (b > 0)
	{
		if(b & 1) res = res * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return res;
}
int get_inv(int x, int p)//费马小定理 
{
	return fast_pow(x, p - 2, p);
}
int n, x, a[N], res, inv[N], p;
map <int, int> mp;
signed main()//折半板子+费马小定理 
{
	n = read();
	p = read();
	x = read();
	for(int i = 0;i < n;i ++) a[i] = read();
	int mid = n / 2;
    if(x >= p) {cout << 0 << "\n";return 0;}
	for(int i = 0;i < (1 << mid);i ++)
	{
		int s = 1;
		for(int j = 0;j < mid;j ++)
		{
			if(1 & (i >> j))
			{
				s *= a[j];
				s = (s % p + p) % p;
			}
		}
		mp[(x * get_inv(s, p) % p)] ++;
	}
	for(int i = 0;i < (1 << (n - mid));i ++)
	{
		int s = 1;
		for(int j = 0;j < n - mid;j ++)
		{
			if(1 & (i >> j))
			{
				s *= a[j + mid];
				s = (s % p + p) % p;
			}
		}
		if(mp.find(s) != mp.end())
		{
			res += mp[s];
			res = (res % MOD + MOD) % MOD;
		}
	}
	(x != 1) ? cout << (res % MOD + MOD) % MOD << "\n" : cout <<  (res + MOD) % MOD - 1 << "\n";
	return 0;
}
6 个赞