史
emm,如你所见,这是一片你所见的算法笔记----平方根!
好吧上一句是废话,这一句也是
平方根算法1——枚举
\sqrt[]8 都会罢(恼),简单来说,你就一个循环,只要循环变量的平方==被开方数,那就返回这个值 ,这里也简单介绍 二分,没错,就是 你学的那个二分 .
没学过二分? 拱出去 猜数游戏 都玩过吧,当你想有快速找出数的时候,不一般都会 选择最中间 的那个值,再进行比较,确定范围,重复操作么?
如裁判给出一个范围 [1,100] 那么,最佳的做法应该是:
- 取 1,100 的中间值—— 50
- 分 3 种情况
1. 如果大了,则范围定为 $(50,100]$ 2. 如果刚刚好,~~啊哈哈,恭喜你,又被你猜中啦~~ 3. 如果小了,则范围定位 $[1,50)$
- 取范围内的中间值,重复操作
而平方根的二分枚举算法也跟猜数游戏差不多,条件判断要改一改,判断 当前枚举的数的平方是否等于被开方数 ,如果等于,返回当前枚举的数,否则,确定范围.
然而很多缺点,它们一般只适用于完全平方数,想要求出 \sqrt[](2) ,还要给他们设置一个增量(看你要求的精度),并且,这,实在是, 太慢了
平方根算法2——牛顿迭代法
没错,就是那个 艾萨克·牛顿
我们接下来就以求 \sqrt[]2 的近似解来了解牛顿迭代法
注意,牛顿迭代法求出的是近似解,而不是真正的值,毕竟 \sqrt[]2 的真实值是无理数吗
一个很突兀的题:
一个二次函数 f(x)=x^2-2 ,草履虫Trxt想知道这个函数的零点的坐标是什么
换句话来说,草履虫所要求的是 x^2-2=0 的实数根是什么。
好了现在 草履虫都知道,这个方程的实数根是 \sqrt[]2
拱出去 我问你,根号2 的近似值是什么
草履虫:std::cout<<std::sqrt(2)<<std::ends; //若只罢,cmath不就行了
拱出去,如果让你手算呢?
我们亲爱的牛顿使用作切线的方式慢慢快速逼近这一串的近似解
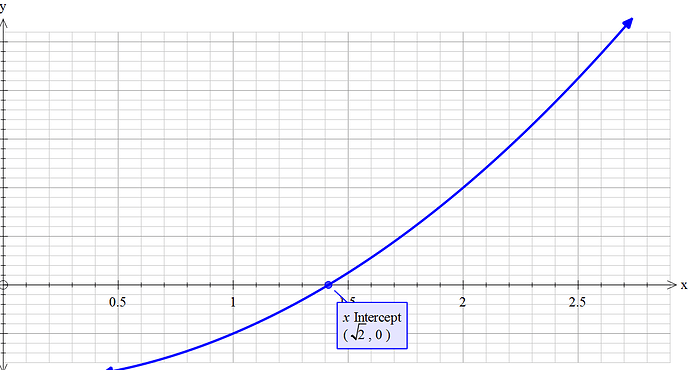
我们先来看二次函数 f(x)=x^2-2
它的图像是
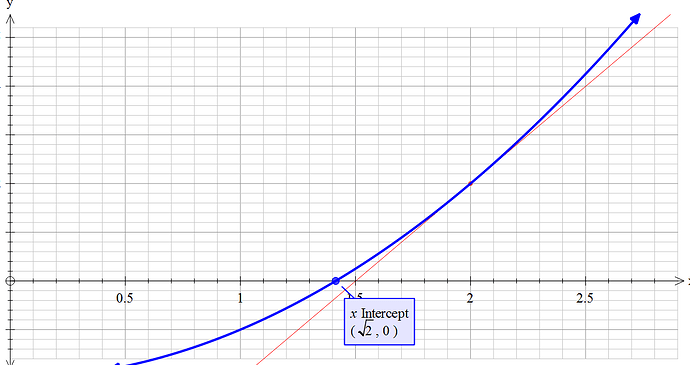
可以看到,它的零点坐标为 ( \sqrt[]2,0 ) ,这时候,我们需要画切线来逼近 \sqrt[]2
牛顿迭代法需要一个初始点(x坐标),这时候我们选择 2
首先我们找出 2 所对应的y值(下图红色空心点的位置),作这一个点的切线(如下图的红线) 至于什么是切线,我会在后文解释 ,这条切线的斜率则是这个点的导数至于什么事导数,我也会在后文解释 ,接下来,我们要求 这条切线与 X轴 的交点
已知两点可以确定一条直线,也可以确定这条直线的斜率 k ,草履虫都知道
k=\dfrac{y_1-y_2}{x_1-x_2}
这里的 P_1(x_1,y_1) 为 初始值2 的函数值在图像上的坐标,为 (2,f(2)) ,而 P_2(x_2,y_2) 为切线与 X轴 的交点,并且 y_2 必然==0 ,k 又是 f(x) 的 一阶导数 f'(x) ,此时x值为 2 ,那么 f(2)=2^2-2=2 , f'(2)=2*2=4 ,因此——
4=\dfrac{2-0}{2-x_2}
移项可得
x_2=2-\dfrac{2}{4}
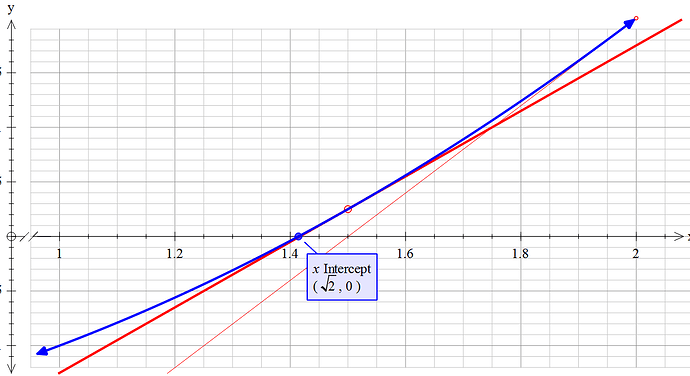
得出交 ♂ 点为 1.5
直接斜率公式一套整这些干什么
此时我们再以1.5为初始点,继续上面的操作——画切线,找交点
如下图加粗红线
x_3=1.5-\dfrac{f(1.5)}{f'(1.5)}
得出的结果大约为1.416667
继续以1.416667作为初始点,继续上面的操作,最终我们将得出$\sqrt2$ 的近似解.
将它们优美地描述成公式:
x_n=x_{n+1}-\dfrac{f(x_{n})}{f'(x_{n})}
好的接下来看一些严谨的解释
一定要记住,牛顿法只不过是求近似解,近似解!所以它将舍弃泰勒展开后的后部分非线性部分
用牛顿迭代法解非线性方程,是把非线性方程
f(x)=0
线性化的一种近似方法。把
f(x) 在点 x_0 的某邻域内展开成 泰勒级数
f(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)(x-x_0)^2}{2!}+...+\dfrac{f^{(n)}(x_0)(x-x_0)^n}{n!}+R_n(x).
取其 线性部分(即泰勒展开的前两项),并令其等于0,即
f(x_0)+f'(x_0)(x-x_0)=0
以此作为非线性方程 f(x)=0 的近似方程
若 f'(x_0)\neq 0 则其解为
x_1=x_0-\dfrac{f(x_0)}{f'(x_0)}
,这样,得到牛顿迭代法的一个迭代关系式:
x_n+1=x_n-\dfrac{f(x_n)}{f'(x_n)}
PS:泰勒展开将这个函数的导函数与其本身关联了起来
非线性方程指的是自变量与因变量之间没有线性关系废话,如 y=x^2、 \alpha=log_e\gamma 等等
好的接下来请看一看牛顿迭代法的公式(我自己写的,所以有些名称起得不规范)
using std::cin;
using std::cout;
inline float Square_Function(float x,int _x)
{
return x * x - (1.0f * _x);
}
inline float DerivativeSF(float x)
{
return 2.0f * x;
}
//sqrt(2)=1.414213562373....
float Sqrt(int _x, float deviation)
{
float x = _x;
do
{
float nxtVal = x - Square_Function(x,_x) / DerivativeSF(x);
x = nxtVal;
} while (x * x - _x > deviation);
return x;
}
int main(int argc, char** argv)
{
int n;
float d;
cin >> n >> d;
float SqrtofN = Sqrt(n, d);
cout.precision(10);
cout << SqrtofN << "\n";
cout.precision(5);
return 0;
}
平方根算法3——平方根倒数快速算法!
首先这是最快的平方根算法,时间复杂度为 \Theta(1) ,秒杀一切草履虫算法
总结一下,平方根倒数快速算法就是 牛顿迭代法 和 二进制 的结合体.
还是以 \sqrt[]2 为例,已知,给牛顿迭代法一个十分接近 \sqrt[]2 的初始值,可以只进行一次迭代,便能得出近似解
因此,要想牛顿迭代法变快,初始值是关键
我们先来看看二进制
草履虫都知道的内容
问你一个问题,电脑是如何存储一个浮点数的呢?
分为 三个部分
- S部分
S部分占一位,全称应该是 sign ,只有 0和1 两个二进制数字,0表示正数,1表示负数
- E部分
记得科学计数法是如何计数的吗?比如我想存放30000000000(3后面100个0),草履虫们一般都会写成 3 \times 10^{100} ,此时,100就是10的指数,而二进制里的E部分,存的就是指数,但是注意,这里真正的值 并不是它所存放的值,而是应该拿 所存放的值 减去 127 ,才是它的真实值,这一部分占8位
- M部分
上文提到了 3 \times 10^{100} ,这里的3是科学计数法里的有效数字部分,而浮点数的二进制形式里的M部分就是有效数字部分,也叫 尾数部分,注意,它所存储的是 小数部分,并且省略了整数部分的1与小数点。这一部分占23位
比如说一个二进制数字: 01000001001001000000000000000000
它应该是多少呢
先拆分一下
S部分是0 \Longrightarrow 它是正数
E部分是10000010,转成 十进制 是 130 , 130-127=3 因此,指数部分为3
M部分是01001000000000000000000,省略后面的0,是01001,转成10在前面补1.01001
知道了这些,那么,这个求这个二进制的值简直是a piece of
vegetablecake.(注意,这里我们已经把M右移23位了)
1.01001_{(2)} \times 2^3 = 1010.01_{(2)} = 10.25_{(10)}
总结出二进制转换成十进制的公式为
N=(-1)^S \times (1.0+\dfrac{M}{2^{23}}) \times 2^{E-127} ①
由于M存储的是 尾数部分的小数部分 ,而计算机里并不会有小数点的出现,因此当我们取出它会特别大![]() ,所以将他除以2^{23},实际上就是将它右移23位,使它变成一个小数。
,所以将他除以2^{23},实际上就是将它右移23位,使它变成一个小数。
然而这个公式有个很致命的缺点:幂运算
2^{23} 可以手算,但是 2^{E-127} 却不行,这比牛顿迭代法还要慢,说好的 \Theta(1) 呢?
别急,发明这个算法的大蛇用一个美丽的函数解决了它
对数!
什么事对数?
a ^x=N ,已知$a$ 和$N$ ,求 x ,这时候,就可以用到对数函数—— log 了
a^x=N , log_a N=x
对数的运算:
log_a(NM)=log_aN+log_aM
log_aN^m=mlog_aN
可以看见,对数将致命的幂运算转成了快速友善的乘运算.
再来复习一下幼儿园学过的幂运算
a^{-1}=\dfrac{1}{a}
a^{\frac{1}{2}}=\sqrt[]a
那么
a^{-\frac{1}{2}}=\dfrac{1}{\sqrt[]a}
这不就是要求的平方根倒数了咩?
因此
log_2a^{-\frac{1}{2}}=-\dfrac{1}{2 }\times log_2a ②
至于这里的底数为什么是2,就下来就会作解释
还记得我们前面所说的二进制吗?它的指数位,也就是E部分,不就是 存的是指数 吗?看到前面的二进制转十进制公式(①式), 2^{E-127} 中的$2$为底数,也就是为什么我们 选2作底数 的原因,而$log$函数,求的就是指数,也就是 E-127
根据对数函数运算的性质(见上文)
log_2(N) = log_2((1.0+\dfrac{M}{2^{23}}) \times 2^{E-127}) = log_2(1.0+\dfrac{M}{2^{23}})+log_2(2^{E-127})=log_2(1.0+\dfrac{M}{2^{23}})+(E-127) ③
公式③里的$N$是公式②里的$a$
是不是感觉很神奇
喜欢这种知识从脑海里流过,不留一丝痕迹的感觉
好的,现在问题来到了 log_2(1.0+\dfrac{M}{2^{23}}) 上面
还记得高2教材上面导数部分中的某一页的旁边的一些不会被注意的文字吗?
它说:微积分的重要思想就是以直代曲,以简代繁,比如我们用3.1415927代替无理数$\pi$ ,用1.618代替黄金比利比例
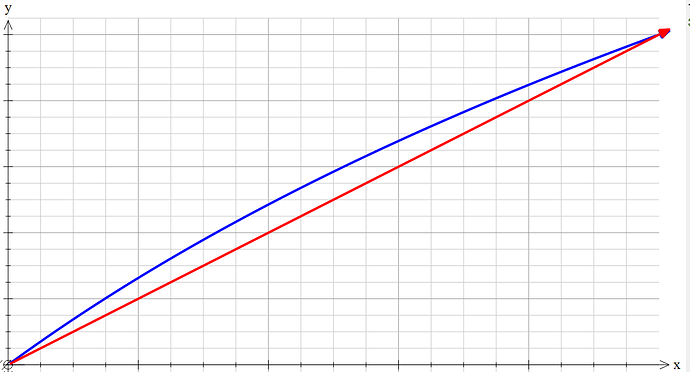
我们来看函数 f(x)=log_2(1+x) 在 [0,1] 之间的图像(如下图蓝线).
由于 \dfrac{M}{2^23} 必然 大于等于0且小于等于1 ,因此我们取的范围也就为 [0,1] .
这时候我们发现,可以用 g(x)=x 来近似代替蓝色曲线 (如红线).
那么, log_2(1+\dfrac{M}{2^{23}}) \approx \dfrac{M}{2^{23}}
整理一下,可以得出
log_2[(1.0+\dfrac{M}{2^{23}}) \times 2^{E-127}]
\approx \dfrac{M}{2^{23}}+E-127
= \dfrac{1}{2^{23}}(2^{23} \times E + M)-127
而括号里的2的23次方乘E加M,不就是浮点数在电脑里的二进制咩?
在这里,大蛇有一次做了一个匪夷所思的行为
设 a 为 y 的平方根倒数,即
log_2 a=-\dfrac{1}{2}log_2y
稍稍转换一下(分别将它们转换成其所对应的对数)
\dfrac{1}{2^{23}} \times a_{(2)} -127=-\dfrac{1}{2}(\dfrac{1}{2^{23}}\times y_{(2)}-127).
移项可得
a_{(2)}=381\times 2^{22}-\dfrac{1}{2}y_{(2)}
而
\dfrac{x}{2}=x>>1
这样子,连 比较慢的除法运算也被转换成快速的位移运算了
而 381 \times 2^{22} 转换成十六进制后为: 5f400000 (不用LaTex是因为它的f跟构式一样,真是必养的).
这里是雷神之锤平方根倒数 快速 算法的源代码
这里的牛顿法可能不太一样,这里的 what the fuck才是重中之重
这里的第9行是将y强制转换成了 可以进行二进制运算 的long类型
这时候身为草履虫的我们就要问了
啊咧咧,为什么这里的0x5f3759df跟我们先前算出来的值不一样呢?
那是因为用来近似代替的函数并没有做到 最佳逼近 曲线函数
这里大蛇用瞪眼法调整了一下,调成了那一串乱码的数字
好吧实际上一开始我也以为大蛇是一步步枚举出这串数字的
实际上
大蛇用到了 切比雪夫最佳逼近。
切比雪夫最佳逼近,它提出任意一个连续函数都可以由一组多项式来逼近
怎么用逼近的自己去网上搜
Ps:搜会死.
最后得出这串魔鬼数字为0x5f3759df.
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
由于本身这个初始值就与真实值极其相似,因此只需进行一次牛顿迭代法就可以得出完全够用的近似解,当然对于今天的计算机,对于较大的值时,也可以再次使用牛顿迭代法.
好的完结撒花,我已经累瘫了,听说算法笔记要一个总结
总结
史
附录
就这构式文章还有附录
导数的物理意义为一个物体的瞬时速度
想想看,幼儿园的时候我们求汽车的平均速度怎么求的,是不是
v=\dfrac{f(t_1)-f(t_2)}{t_1-t_2}
这里的 f(x) 函数为在 x 秒时,所对应的路程
而所谓瞬时速度,就是在一个无穷小的时间范围内,它的平均速度
因此
lim_{x\to0} v=\dfrac{f(x+\Delta x)-f(x)}{\Delta x}
而导数的几何意义,就是上文提到过的切线
草履虫都知道:两点可以确定一条直线,当两点沿着函数曲线越来越接近的时候,以至于其距离无限趋近于0的时候,这一条直线就是这个点的切线,而这这个点的切线的斜率就是这个点的导数,也等于这个角的 tan 值(根据 tan 函数的定义和斜率公式就可以推导出:他们三个是等价的)