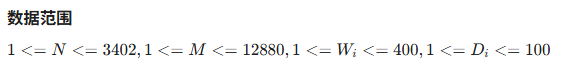基础过渡——背包

[王皓宇 (*对方不愿透露姓名*)]

废话少说，先看题目

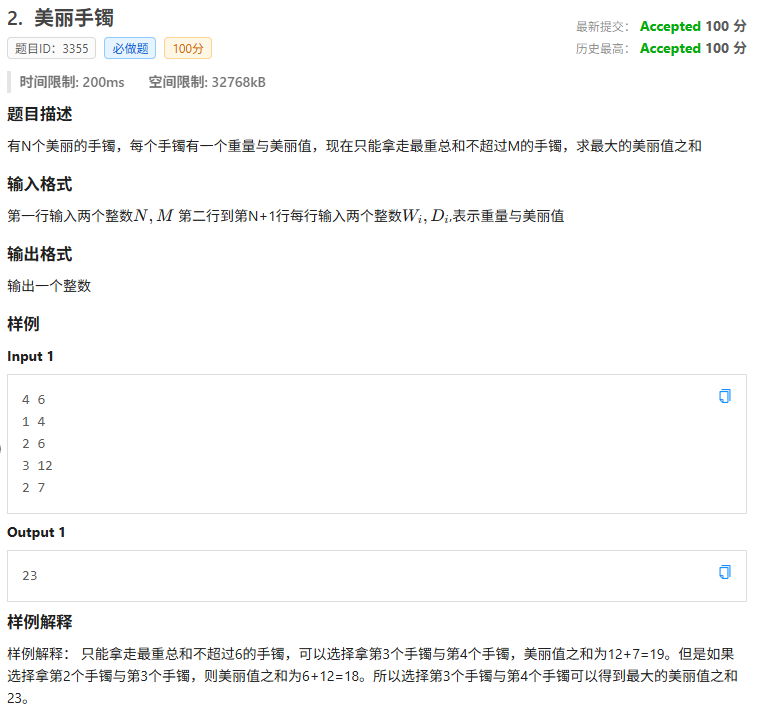
拿到题目第一眼

暴搜！！！

考虑每一个手镯的2种情况（拿 或 不拿）

OK呀 直接O(2ⁿ)，别急，看看这个↓

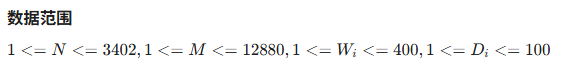
觉得不够大？

也就是比1e1000还大，也许你现在运行，到宇宙毁灭就出结果了

那怎么办？

#include<bits/stdc++.h>
using namespace std;

int n = 0,m = 0,ans = 0;
int ti[3500] = {0},v[3500] = {0},dp[100001] = {0};

int main()
{
	cin>>n>>m;
	for(int i = 1;i <= n;i++)
	{
		cin>>ti[i]>>v[i];
	}
	for(int i = 1;i <= n;i++)
	{
		for(int j = m;j >= ti[i];j--)
		{	
			dp[j] = max(dp[j] , v[i] + dp[j - ti[i]]);
		}
	}
	for(int i = 1;i <= m;i++)
    {
        ans = max(ans,dp[i]);
    }
    cout<<ans;
	return 0;
}//非常巧妙の设计

原理是什么？？？

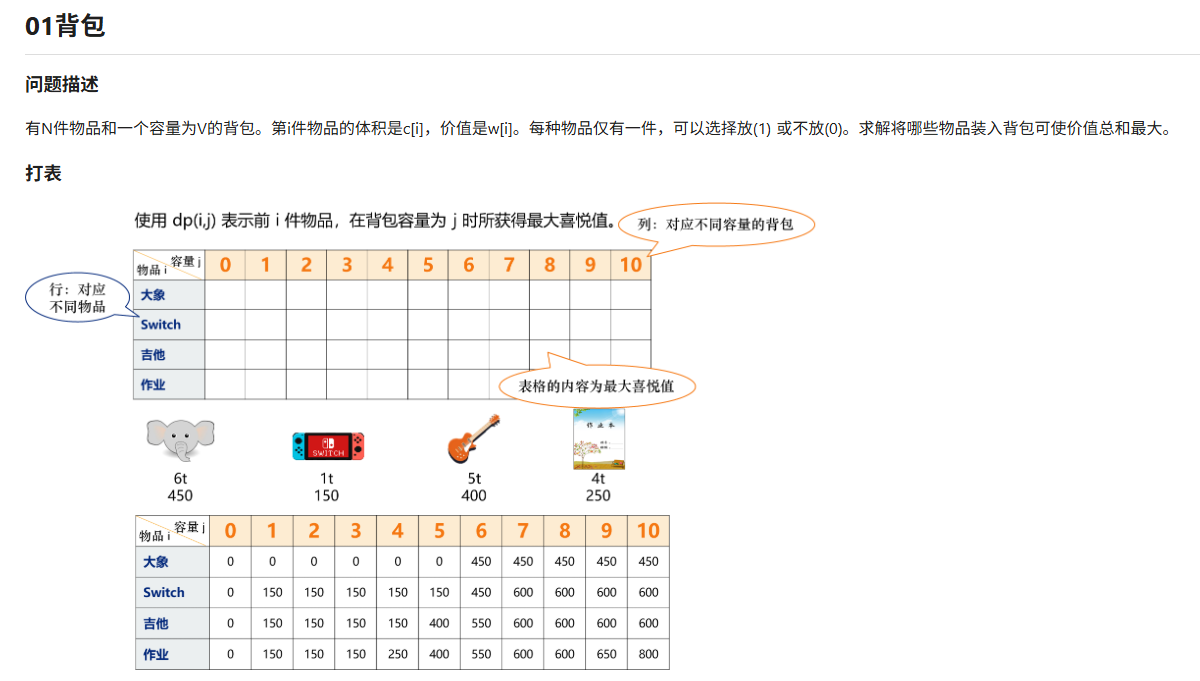
其实在考虑当前物品是否拿下时，我们仅仅需要找前面最有用的值

使其对答案的贡献尽量大

在拥有更优解时，我们就会舍弃旧的答案。

不然那些旧的答案就会陪你到宇宙毁灭

重新看代码

#include<bits/stdc++.h>
using namespace std;

int n = 0,m = 0,ans = 0;
int ti[3500] = {0},v[3500] = {0},dp[100001] = {0};//dp[i] 表示重量 i 的情况下最大价值

int main()
{
	cin>>n>>m;
	for(int i = 1;i <= n;i++)
	{
		cin>>ti[i]>>v[i];
	}
	for(int i = 1;i <= n;i++)
	{
		for(int j = m;j >= ti[i];j--)//此时对于0<i<j,dp[i]尚未改变，所以不会有多次拿
		{	
			dp[j] = max(dp[j] , v[i] + dp[j - ti[i]]);//更新重量 j 的情况下最大价值
		}
	}
	for(int i = 1;i <= m;i++)
    {
        ans = max(ans,dp[i]);
    }
    cout<<ans;
	return 0;
}

其实背包后面的动态规划才是重点

但由于篇幅有限，加上树上DP，线段树优化DP根本就不是基础组该学的，所以下（jiang）次（ge）再（sha）讲（ya）

撒花