十、 图论
-
基本概念/术语
-
顶点/节点(Vertex/Node),简称点。
-
边(Edge):节点之间的连线。
-
完全图:任意两点都有边相连,一个 n 个节点完全图的边数 C_n^2= \dfrac{n(n-1)}{2} 。(对于组合数 C^2_n 的具体说明详见“数学”部分)
-
简单路径:两点之间通过不重复的边相连。
-
连通图:任意两点都可以直接/间接到达,注意区别于完全图,完全图属于连通图,连通图不一定属于完全图。
-
有向图:边是有方向的( e = u\rightarrow v )。
-
无向图:边是无方向的( e = u\leftrightarrow v )。
-
环:对于一个回路 w ,若 v_0=v_k 是该回路点序列中唯一重复出现的点对,则 w 是一个环。
特别的,如果环 w 只有一个点,则被称为“自环,即 e=(u,v), u=v 。
-
入度:以顶点 v 为终点的边的条数为该节点的入度。
-
出度:以顶点 v 为起点的边的条数为该节点的出度。
-
-
树
-
基本概念/术语
-
树:一个长得像真实生活中 倒置(即根在上、叶子在下) 的树的图,任意两点之间的简单路径有且只有一条。树是一棵连通且无环的图,边数 =n−1 。
-
根节点:树最上层的节点,一棵树有且只有一个。
-
深度:到根结点的路径上的边数。
-
高度:所有结点的深度的最大值。
-
叶节点:没有子结点的结点。
-
父亲:对于除根以外的每个结点,从该结点到根路径上的第二个结点。根结点没有父结点。
-
祖先:一个结点到根结点的路径上,除了它本身外的结点。根结点的祖先集合为空。
-
子节点:如果 u 是 v 的父亲,那么 v 是 u 的子结点。子结点的顺序一般不加以区分,二叉树是一个例外,有左儿子/右儿子之分。
-
兄弟:同一个父亲的多个子结点互为兄弟。
-
后代:如果 u 是 v 的祖先,那么 v 是 u 的后代。
-
子树:删掉与父亲相连的边后,该结点所在的子图。
-
-
二叉树
-
前/先序遍历:根 \rightarrow 左子树/儿子 \rightarrow 右子树/儿子。
-
中序遍历:左子树/儿子 \rightarrow 根 \rightarrow 右子树/儿子。
-
后序遍历:左子树/儿子 \rightarrow 右子树/儿子 \rightarrow 根。
-
遍历的特殊结论
-
前/先序遍历 + 中序遍历 = 确定二叉树。
-
后序遍历 + 中序遍历 = 确定二叉树。
-
-
特殊的二叉树及其性质
- 满二叉树/完美二叉树:所有叶结点的深度均相同的二叉树称为满二叉树/完美二叉树。
满二叉树的第 k 层有 2^{k-1} 个节点,任意 k 层二叉树最多有 2^{k-1} 个节点。
若在任意一棵满二叉树中,有 n_0 个叶子节点,有 n_2 个度为 2 的节点,则有 $n_0=n_2+1$。
n 个节点的满二叉树深为 \log n+1
- 完全二叉树:只有最下面两层结点的度数可以小于 $2$,且最下面一层的结点都集中在该层的最左侧。
-
对于一棵满二叉树/完美二叉树,其深度为 k ,则其节点总数为 2^k-1 ,此结论可逆。
-
对于一棵满二叉树/完美二叉树/完全二叉树,若任意节点(除叶节点外)的编号为 i ,其左儿子的编号为 2i ,右儿子的编号为 2i + 1 。此结论可逆,证明显然。
二叉树的第 k 层至多有 2^{i-1}(i\ge1) 个节点。
-
-
-
习题
-
栈
-
定义/术语
-
定义:有一叠碗,每一次取的时候取最上面的出来,放的时候放到最上面,先进来的后出去,后进来的先出去,这就是后进先出(last in first out)表,简称 LIFO 表。
-
栈顶:栈最顶端的元素。
-
栈底:栈最底端的元素。
-
-
操作
-
push(x)往栈顶前添加一个元素 $x$。 -
pop()从栈顶弹出(删除)一个元素。 -
top()返回栈顶的值。 -
empty()返回是否为空。(1 为空,$0$ 为非空) -
size()返回栈里的元素个数。
-
-
-
队列
-
定义/术语
-
定义: 与生活中的队列相同,一条队伍,没有人会插队,大家都按队伍的规矩排好。先进来的先出去,后进来的后出去,这就是先进先出(first in first out)表,简称 FIFO 表。
-
队首/队头:队列的第一项。
-
队尾:队列的最后一项。
-
操作
-
push(x)往队尾后添加一个元素 x 。 -
pop()从队首弹出(删除)一个元素。 -
front()返回队首的值。 -
empty()返回是否为空。( 1 为空 0 为非空 ) -
size()返回队列里的元素个数。
-
-
-
链表
-
定义/特点
-
定义:链表和数组都可用于存储数据,其中链表通过指针来连接元素,而数组则是把所有元素按次序依次存储。
-
链表可以方便地删除、插入数据,操作次数是 O(1) ,但是访问任意数据时操作次数是 O(n) 。
-
链表不可以随机访问任意数据!
-
-
习题
-
-
字符串
-
定义:字符串指一串字符组成的串。
-
子串:子串被定义为字符串中任意个连续的字符组成的子序列,子串个数 =\dfrac{n(n+1)}{2}+1 ,非空子串的个数 =\dfrac{n(n+1)}{2} (无非就是少了空子串的 +1 )
-
前/中/后缀表达式:
-
前缀表达式:一种没有括号的表达式,与中缀表达式不同的是,将运算符写在前面,操作数写在后面。如:前缀表达式 -1+2\,\,\,3 的中缀形式为 1-(2+3) 。
-
中缀表达式:与平常使用的表达式相同,有括号且运算符在操作数中间。
-
后缀表达式:与前缀表达式相反,将操作数写在前面,运算符写在后面。如:后缀表达式 1\,\,\,2\,\,\,3+- 的中缀形式为 1-(2+3) 。
-
前/中/后缀表达式的转化
-
前/后缀表达式转中缀表达式
-
画出表达式树:表达式树是一种特殊的树,叶节点是操作数,其他节点为运算符
-
将表达式树前序遍历,可得前缀表达式;中序遍历可得中缀表达式;后序遍历可得后缀表达式。
-
-
中缀表达式转前/后缀表达式
-
给中缀表达式加上括号:
1-2+3\rightarrow ((1-2)+3) -
把运算符移到括号前/后面(移到前面为前缀表达式,反之亦然):
(1-(2+3))\rightarrow ((12)-3)+ -
删去括号,剩下的即为最终解:
(1(23)+)-\rightarrow 12-3+
也可以用上文的“表达式树”做,比较复杂,推荐以上加括号的方法。
-
-
-
-
十一、排列组合
-
加法原理:完成一项工作有 n 种方法, a_i(1\le i \le n) 代表完成第 i 类方法的数目,共有 S=a_1+a_2+\cdots+a_{n-1}+a_n 种不同的方法。
-
乘法原理:完成一项工作有 n 个步骤, a_i(1\le i \le n) 代表完成第 i 个步骤的数目,共有 S=a_1\times a_2\times \cdots\times a_{n-1}\times a_n 种不同的方法。
-
排列(Arrangement/Permutation)
-
定义:从 n 个不同元素中,任取 m ( m\le n )个元素按照一定的顺序排成一列,读做从 n 个不同元素中取出 m 个元素的一个排列,记为 A_n^m (或 P_n^m )。
-
计算公式: A_n^m=n(n-1)(n-2)\cdots(n-m+1)=\dfrac{n!}{(n-m)!}
其中, ! 表示阶乘,例如 6!=1\times 2 \times 3\times 4\times 5\times 6 ,特别规定 0!=1。
-
证明:第 1 个位置可以选 n 个元素,第 2 个位置由于先前已经选了一个,还可以选 (n-1) 个元素,以此类推,第 m 个可以选 (n-m+1) 个元素。又根据上述的乘法原理,将所有的选法串联起来,因此得到上式。
-
全排列:排列的一种特殊情况,此时 m=n,n-m=0 ,刚刚规定过 0!=1 ,所以 A_n^n=n!=1\times 2\times 3\cdots \times n 。
-
-
组合(Combination)
-
定义:从 n 个不同元素中,任取 m(m\le n) 个元素组成一个集合,读做从 n 个不同元素中取出 m 个元素的组合。即不关心被选元素的顺序。记为 C_n^m 。
-
公式: C_n^m=\dfrac{A_n^m}{m!}=\dfrac{n!}{m!(n-m)!}
-
证明:如果 n 个元素中选 m 个且关心顺序,为 A_n^m 。但是此时不关心顺序了,就需要去掉重复的,同样选出来的 m 个元素,还要进行全排列,即除掉 m! ,因此展开后得到上式。
组合数也常用 \dbinom{n}{m} 表示,读作“ n 选 m ”,更为清晰明了。
-
-
排列组合九大解题技巧(按个人认为的理解难度排序)
-
先选后排:先将元素选出来,再进行排列,非常有效的降低问题的复杂度。
-
特殊优先:特殊元素,优先处理;特殊位置,优先考虑。
-
分排用直排: n 个元素,从中选出 m 个,将这 m 个元素排成若干排。分排问题的排列可以看做一排,避免考虑了复杂的前后排列,简化了问题。
S=A_n^m
-
分类法:当计算符合条件的数目比计算不符合条件数目简单时,将问题分成若干类,逐个求解,与“排除法”相对。
-
排除法:当计算符合条件的数目比计算不符合条件数目复杂时,简称正难则反。排除不符合要求的,剩下的就是符合题目要求的。与“分类法”相对。
-
捆绑法: n 个不同元素排成一列,要求 m 个元素必须相邻。可以特殊优先,把 m 个元素捆绑在一块单独处理。
S=A_{n-m+1}^{n-m+1}\times A_m^m
-
插空法: n 个不同元素排成一列,要求 m 个元素不能相邻。先把不用特殊处理的元素进行排列,再把甲乙进行插空。
S=A_{n-m}^{n-m}\times A_{n-1}^{m}
-
隔板法/插板法:将 n 个相同元素分成 m 组,每组至少有一个元素。相当于把 m-1 个隔板插到 n 个元素形成的 n-1 个空隙里。
S=C_{n-1}^{m-1}
-
定序: n 个元素的全排列中有 m 个元素必须定序排列,这 m 个元素相邻或不相邻不受限制。
S=\dfrac{A_n^n}{A_m^m}
-
-
习题
-
十二、复杂度
一个问题有很多种不同的算法,如何评价一个算法的好坏呢?这就需要时间复杂度和空间复杂度来衡量了。
-
定义
渐进时间复杂度,用符号 \mathcal{O} 表示。一个算法里语句的执行次数可以用一个式子表示,取这个式子的最高次项且忽略系数表示该算法的时间复杂度。例如,一个程序的语句执行次数为 2n+3n^2+9+8n ,则该算法的时间复杂度为 \mathcal{O}(n^2) 。
-
常量
常量,即永远不变的量,例如, 1 就是 1 ,它永远不可能等于 2 。在时间复杂度里,只要不随着输入数据规模的大小增长而增长的量,就被称之为常量,在计算中省去不写。
特别的,如果代码中出现了宏定义,那么宏定义的值依旧是常量,因为它不随着输入数据规模的大小而改变。
-
示例
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) cin >> a[i][j];本代码中,
cin >> a[i][j]执行了 n^2 次,所以时间复杂度为 \mathcal{O}(n^2) 。for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) cin >> a[i][j]; for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) cin >> b[i][j];本代码中,
cin >> a[i][j]执行了 n^2 次,cin >> b[i][j]也执行了 n^2 次,忽略系数,时间复杂度还是 \mathcal{O}(n^2) 。for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) cin >> a[i][j]; for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) for(int k = 1; k <= n; k++) cin >> b[i][j];本代码中,
cin >> a[i][j]执行了 n^2 次,cin >> b[i][j]执行了 n^3 次,取最高次项,时间复杂度是 \mathcal{O}(n^3) 。 -
符号
T(n) 表示时间复杂度, T(n)= 后跟一个符号:
\Theta ,
theta,等于。\mathcal{O} (也可写作 O ),
big-oh,小于等于。\Omega ,
big-omega大于等于。o ,
small-oh小于。\omega ,
small_omega大于。 -
非递归程序的时间复杂度的计算
非递归程序的时间复杂度计算一般都比较简单,直接数循环。大多数算法都适用于此,但是也有例外,例如二分等,需要特别留心。
-
递归程序&主定理
假设某算法的计算时间表示为递归式:
T(n)=2T(\dfrac{n}{2})+n\operatorname{log}nT(1)=1求该算法的时间复杂度。
- 直接代入递归求解
虽然此方法计算量较大,但是是初学者不二的选择。如果追求卷面,可以学习主定理。
- 主定理:将一个规模为 n 的问题,分治成 a 个 \lceil\dfrac{n}{b}\rceil 的子问题,每次带来的额外计算为 \mathcal{O}(n^d) ,可得到以下关系式:
-
空间复杂度
-
定义:空间复杂度较时间复杂度来说简单许多,可以直接数。符号同时间复杂度。
-
计算
\begin{matrix} &\text{变量 int a}&\text{一维数组 int a[n]}&\text{二维数组 int a[n][n]}&\cdots\\ \text{空间复杂度}&\mathcal{O}(1)&\mathcal{O}(n)&\mathcal{O}(n^2)&\cdots\\ \end{matrix}可见,只需要数数组有几维即可,其他注意事项(如常数等)与时间复杂度相同。
-
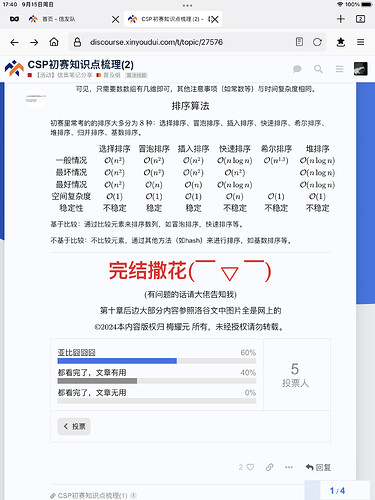
初赛里常考的的排序大多分为 8 种:选择排序、冒泡排序、插入排序、快速排序、希尔排序、堆排序、归并排序、基数排序。
基于比较:通过比较元素来排序数列,如冒泡排序,快速排序等。
不基于比较:不比较元素,通过其他方法(如hash)来进行排序,如基数排序等。
- 都看完了,文章有用
- 都看完了,文章无用
- 亚比囧囧囧