姓名: 王梓涵
赛道: 提高组
类型: 算法技能
分块与珂朵莉树
关键词: 区间推平、分块、split
首先区间问题是在比赛中经常出现的一种题型,而用好写的方法解决问题,是在比赛策略中的最佳选择,而我今天讲的两种算法是在区间问题中好理解的两种的算法,在一些题目中,他们可以拿到很高的分数,在一些题目中他们是正解,当然在一些题目中他们还是最优解,接下来我通过讲解算法与相关例题,来教会大家这两种算法。
本片笔记主要分为 3 部分:
-
各种概念讲解加模板题和模板代码
-
各种概念的练习题
-
总结
各种概念讲解加模板题和模板代码:
分块引入:
分块的定义:分块,顾名思义就是将一个序列切成若干块,根据每一块来维护信息,以达到提高时间复杂度的效果。这也是一种结合了纯粹暴力和前缀和思想的数据结构。用分块解决的题目一般较为复杂,时间复杂度修改查询都是 O(\sqrt n) 的。
引入题目:
给你一个序列 a ,要求支持单点修改,查询区间和, n\le10^{5} 。
我们考虑暴力地解决这个问题:一个最直观的想法,当然就是直接模拟了。区间和的查询,直接暴力从左往右枚举。那么好我们发现,查询操作,时间复杂度太高了!于是我们想到了另一个操作:对整个序列做前缀和。这样区间和就转化为 s_r - s_{l - 1} 了。那么可以发现,修改操作,时间复杂度太高了!
那么,我们该何去何从?(当然是写树状数组了 bushi )
我们考虑这样一件事情,我们把整个序列分成若干块,我们维护整个块的前缀和,那么区间查询,就转化为求一段区间内的区间和,显然可以发现,这样做时间复杂度已经变为了 O(\sqrt n) ,其中 n 为序列长度,接下来我给大家画一张图助于大家的理解:
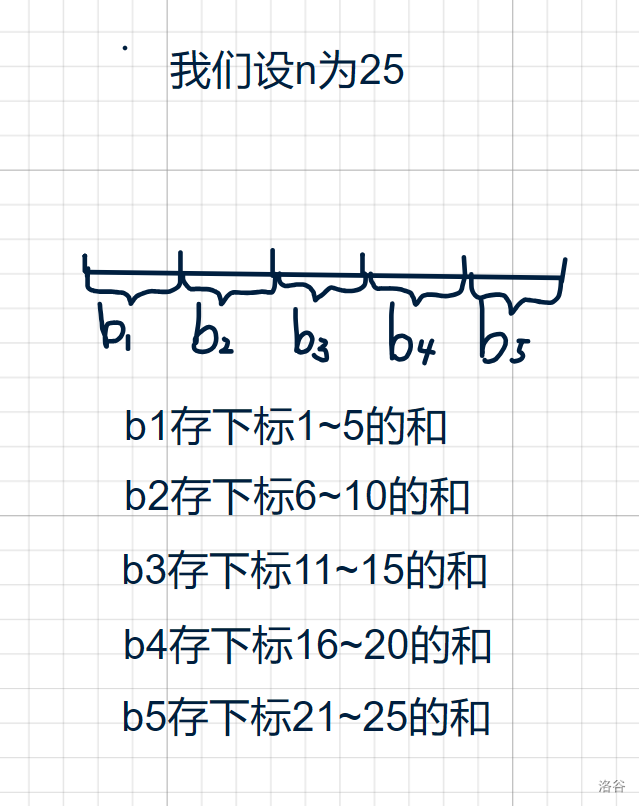
以上的 b 数组就是用来存每个块内的总和,显然会发现,这样子的块最多会有 \left \lceil \sqrt n \right \rceil 个,但是后面我们又会发现一个问题,在查询的时候,可能有些块,不用算整个块的和,需要一部分,这时候该怎么办呢?想处理这种问题最好的办法,因为这种情况只可能出现在两端,当然如果这是查询区间至少到了 3 个块上的情况,所以我们需要将两端进行特殊处理,通过前缀和去计算块一部分的贡献,即总和。
给大家放一个本道题的代码,尽可当作模板来看,在后面的分块例题中,就不会再放代码了:
void init()//分块小练习
{
int sqr = sqrt(n);//计算块数
tot = (n - 1) / sqr + 1;//块长
for (int i = 1;i <= tot; ++ i)
{
l[i] = r[i - 1] + 1;//每个块的左坐标
r[i] = sqr * i;//每个块的右坐标
}
r[tot] = n;//最后一个块的右坐标,因为最后一个块可能不完整
for (int i = 1;i <= tot; ++ i)
{
for (int j = l[i];j <= r[i]; ++ j)
{
sum[i] += a[j];//第i个块中的前缀和
belong[j] = i;//序列中第j个数属于块i
}
dp[i] = dp[i - 1] + sum[i];//前i个块的前缀和
}
}
void modify(int x, int k)//单点修改
{
sum[belong[x]] += k;//更新块内前缀和
a[x] += k;//更新序列
for (int i = belong[x];i <= tot; ++ i)
{
dp[i] += k;//将后面影响的区间修改
}
}
int query(int x, int y)
{
int res = 0;
if(belong[x] == belong[y])//两个点在同一个块内
{
for (int i = x;i <= y; ++ i)
{
res += a[i];
}
return res;
}
res = dp[belong[y] - 1] - dp[belong[x]];//计算除两端以外的总和
for(int i = x;i <= r[belong[x]]; ++ i)//单独处理左端
{
res += a[i];
}
for(int i = l[belong[y]];i <= y; ++ i)//单独处理右端
{
res += a[i];
}
return res;
}
提交上去一看不仅 AC 了,而且跑的速度比树状数组要快一倍。
珂朵莉树/颜色段均摊:
珂朵莉树(颜色段均摊)首见于 CF896C。
需要的前置知识:std::set(不过其实也不需要)
大致思想:珂朵莉树的想法,其实是将区间化作一个个三元组 (l,r,v) 。分别表示区间的左右端点,和区间上的值。然后用 set 维护,按照左端点第一关键字排序就行。区间不重不漏的覆盖了 [1,n] 中所有位置。不会有两个区间出现重叠的情况。对于区间推平(赋值)操作,我们设操作为 [l,r,v] 。则在 set 中,我们要分离开端点和对应区间以便于操作。
我们分离开 r , l-1 的位置。然后删掉两个迭代器中所有区间,再插入 [l,r] 。为什么先分离 r 呢?这是因为,在 l-1 分离后,再分离 r 可能导致 l 的迭代器失效(最简单的, l-1=1,r=2,l_1=0,r_1=3 ,首次分离返回 [2,3] ,再分会 erase 掉),而先分离 r ,不会有这种问题。
类似的对于区间求和,我们分离开 r , l-1 的位置,然后得到对应的迭代器,遍历就行。之后用迭代器遍历的办法,就可以得到所有的区间了 for(auto it=itl;it!=itr;++it) 。
珂朵莉树支持几乎所有的区间操作,你几乎可以看做是暴力进行。因为和暴力的区别,就在于分段了而已。
在有大量区间赋值操作,并保证数据随机的时候,使用珂朵莉树将会大幅降低代码难度,均摊时间复杂度 O(m \log \log n) 。这是由于区间数量会很快退化成 \log\log n 个。具体证明请看 珂朵莉树的复杂度分析 。空间复杂度,是 O(n) 的。因为最多只有 n 个区间。
int qpow(int a, int b, int p)
{
a %= p;
int res = 1;
for (; b; b >>= 1, a = a * a % p)
if (b & 1)
res = res * a % p;
return res;
}
struct odt_t
{
struct node
{
int l, r;
mutable int v;
int len() const { return r - l + 1; }
node(int l = 0, int r = 0, int v = 0) : l(l), r(r), v(v) {}
friend bool operator<(const node &a, const node &b) { return a.l < b.l; }
};
set<node> s;
set<node>::iterator split(int x)
{ // 目的:分离 [l,r] 为 [l,x-1],[x,r],返回后者迭代器
auto it = --s.upper_bound(node(x)); // 找到左区间
if (it->l == x)
return it;
auto [l, r, v] = *it;
s.erase(it);
s.emplace(l, x - 1, v);
return s.emplace(x, r, v).fi; // first 是迭代器
}
#define SPLIT auto itr = split(r + 1), itl = split(l) // 宏定义缩短码量
void assign(int l, int r, int x)
{ // 区间赋值
SPLIT;
s.erase(itl, itr);
s.emplace(l, r, x);
}
void add(int l, int r, int x)
{ // 区间加
SPLIT;
for (; itl != itr; ++itl)
itl->v += x;
}
int ask(int l, int r, int k)
{ // 区间第 k 小
// 每次减掉区间长度,看什么时候降到0即可
SPLIT;
vector<pair<int, int>> buc;
for (; itl != itr; ++itl)
buc.pb({itl->v, itl->len()});
sort(buc.begin(), buc.end()); // 按照大小排序
for (auto [u, len] : buc)
if ((k -= len) <= 0)
return u;
return -1;
}
int askk(int l, int r, int k, int p)
{ // 区间k次方和
SPLIT;
int res = 0;
for (; itl != itr; ++itl)
(res += qpow(itl->v, k, p) * itl->len() % p) %= p;
return res;
}
void insert(int l, int r, int v) { s.emplace(l, r, v); } // 看着舒服的插入
} odt;
各种概念的练习题:
分块练习题:
支持区间修改,查询区间和。
首先,就是我们考虑暴力怎么做(别告诉我你会线段树),每次循环一个区间 [l,r] ,暴力的修改上面的值。查询也是暴力。时间显然超时。我们考虑转变一个思路:既然这样暴力不行,我们把整个区间 [1,n] ,分成若干块之后,再暴力,时间还会不会超呢?
设块长为 S ,则区间修改,就是对于整块的部分,不做真的修改。我们对于每个块设置一个标记 add ,表示该块被整体增加的量。同样的和之前,设置一个 sum 表示一个块的和。我们发现,标记不用实际加到每个数上面。对于整块的修改,我们增加 add\gets add+t 。对于零散的修改,我们修改那些位置,并增加区间和。整体的查询,我们发现整块的和是 sum+add\times len 。零散的和,就是 \sum a_i+len'\times add 。
我们分析复杂度。设要修改的区间为 $[l,r]$,假设他跨了若干个整块,并且在两边有两个不完整的块,那么我们对于整块的修改,单次是 O(1) 的,一共最多有 \left\lfloor\frac{n}{S}\right\rfloor 个块。而对于两边的块,我们发现,最多有 2S 的长度。所以修改的时间复杂度为 O(\left\lfloor\frac{n}{S}\right\rfloor+2S) 。查询的时间,也是一样的。于是,我们要最小化 \frac{n}{S}+2S 。一般取 S=\sqrt n ,就可以满足要求。此时复杂度为 O(m\sqrt n) 。不会超时。
要求区间加 w ,区间查询大于某给定的数 k 的数量。
我们考虑对序列进行类似排序的操作,把每一段都分别再开个排序后的数组。之后查询就是对于整块,再里面二分对应的 k-tag_x 的数量,对于两侧的,暴力处理就行。修改对于整块的,将 tag_x 加上 w 即可,在两边的,暴力加就行,注意两边加完后,要重新处理排序后的数组。
你需要维护两种操作:
-
将其中一个颜色反转,即黑变白,白变黑。
-
找到点 1 到点 u 的路径中,出现的第一个黑点,不存在,则输出
-1。
总结的来说就是大水题,只需要用分块维护每一条链中,升读最小的黑点,用树链剖分处理各类信息即可。
给定你一个序列,你需要维护区间数开平方与区间求和两个操作。
首先不得不说这道题目真的是太简单了,甚至连懒标记都不需要打,首先你需要维护每个块内的和,以及块的前缀和,记录每个位置属于第几个块,以上操作我们需要提前预处理。再接着就是修改操作,对于每一个需要开平方的数,只需要一一暴力修改即可,在修改的同时更新前缀和,但是光光这样做,复杂度类似 O(n ^ 2) ,这时候,就要用到我们的优化剪枝了,因为我们知道,一个数连续开平方,最终一定会变成 永久 的 1 ,那么我们可以在修改的地方开始优化,如果一个块内的和与块长相等,那么我们就不用进行修改,因为即使继续开平方,也还是 1 ,每个数的大小和块内总和是不会改变的。而区间求和操作的代码就与树状数组模板题一样了,先利用块前缀和,算出中间的总和,暴力计算两端的块内和即可。
游戏一开始,Lostmonkey 在地上沿着一条直线摆上 n 个装置,每个装置设定初始弹力系数 $k_i$,当绵羊达到第 i 个装置时,它会往后弹 k_i 步,达到第 i+k_i 个装置,若不存在第 i+k_i 个装置,则绵羊被弹飞。
绵羊想知道当它从第 i 个装置起步时,被弹几次后会被弹飞。为了使得游戏更有趣,Lostmonkey 可以修改某个弹力装置的弹力系数,任何时候弹力系数均为正整数。
这道题目,你会发现,用分块加上类似 dp 的思想,会有一种十分奇妙的方法,首先,我们先用分块维护出每个长度为 \sqrt n 的块中,分别包含哪些位置(编号)。我们设 a_i 为点 i 跳出当前块后,会跳到哪一个位置, nex_i 为点 i 跳出它所在的块一共需要多少次。在操作前先对于整个去进行预处理,接着,在每次修改操作时,对于一个块去更新即可,因为每个块在查询时互不影响,因此只要去看修改的点所在的块,进行修改即可,修改时间复杂度约为 O(\log n) ,查询就用地推的信息,不断地跳跃,知道跳出了范围后即可停下,查询的代码放一下:
int ask(int k)
{
int ans = 0, u = k;
while (u < n)
{
ans += nex[u];//记录跳出当前块的次数
u = p[u];//找到跳出块后,会到哪一个位置
}
return ans;
}
此操作单次时间复杂度为 O(\log n) 。
总时间复杂度约为 O(m \log n) ,显然可以通过。
第二分块
问题描述:给点序列 a ,有两种操作,
op=1 :对于 [l,r] 中大于 x 的元素减 x 。
op=2 ,查询 [l,r] 中等于 x 的元素个数。
1\le n\le10^6 , 1\le m\le10^5,0\le x\le 10^5+1 。
设 n, V 同阶( V 是值域)。
考虑用分块做。我们发现区间最大值单调下降。
具体地,分为整块操作和散块操作。
- 整块操作
考虑维护区块最大值 mx ,对每次修改的 x 分类讨论。
- 若 mx\le x ,则不用修改,时间 O(1) 。
- 若 x<mx\le2x ,则最大值至少降到 x 。时间 O(mx-x)\le O(x) 。
- 若 mx>2x ,正难则反,考虑全局减 x (标记永久化 O(1) ) ,对于 [0,x] 中的数 t\gets t+x 。 O(x) 。
综合起来,时间复杂度为 O(V\sqrt n\alpha(n)) 。
那么说了这么久,到底怎么维护每个值的信息呢?
考虑开一棵记录权值的个数的并查集。
具体地,把值相同的位置下标合并到一起,对于每个代表元,记录其代表的值和个数。
可以发现,区间减法(加法)就是在把某些代表元,合并到另一些代表元中的过程。并且合并后,原来的信息清空,并入改变后的值对应的集合。而并查集的合并,并不会影响到什么额外的事情,因为并查集记录的是下标,下标是两两不同的。于是对于每个块,记录每个值对应位置,个数的空间是 O(V\sqrt n) 的,在这里不能接受(会MLE),优化用到一个性质,就是块与块之间,可以独立开算对于每个答案的贡献,并且不会冲突。于是空间复杂度降为 O(V) 。
- 散块操作
重构散块,先在并查集上获取值,并且清除得到的值的根和个数,清除后再减去减标记。因为并查集维护的值是基于减标记之前的。之后清空减标记。修改完后重新求每个值的个数,区间最大值等,重新处理并查集。时间复杂度
O(n\sqrt n\alpha(n)) 。
参考资料:第二分块学习笔记
珂朵莉树/颜色段均摊练习题:
给一棵无根树,要求两种操作
-
u, v 简单路径上所有点染成颜色 c 。
-
查询 u,v 颜色段数目。
提到颜色段,我们立马想到,可以用 ODT 解决。其他和树剖板子一样,需要注意的是,这次要对 u,v 分开统计,不能用 swap(u, v) 之类的操作,我们需要记录下 u, v 跳链过程中最后一段的颜色,如果发现和上面一段相同,则答案 $-1$。最后一次合并过后需要判断是否 u,v 最上面的颜色,是一样的。因为之前一直是分开询问,这次 u, v 在一条链上了,最终如果两个颜色相同,答案要 -1 。
CF915E Physical Education Lessons
在这道题目中,你需要支持两个区间推平操作,很显然,珂朵莉树的裸题,只需要在每次操作后更新工作日数量即可,比模板题简单多了,就不细讲了。
这道题目需要维护的操作有些多,不过纯水题,首先操作 1 区间求和,因为一个块内的数值是相同的,所以对于每一个块, O(1) 计算出块内和,将整个区间分块扫一遍,平均 时间复杂度为 O(\log n) 。接着是操作 2 区间推平,珂朵莉树决定时间复杂度的重点操作(灵魂),这个操作就不讲了。操作 3 区间加法,我们会发现一个事情,同一个块内的值加上同一个数,所有数还是相等的,所以不用更新块,只需修改块内的值即可。操作 4 区间复制,这个操作我们只需要用最朴素的方法,将需要复制的区间复制到一个数组内,然后根据需要被复制掉的区间,他在序列中的位置,与复制序列中位置的相差去添加,将原本的删去即可。操作 5 也是类似,把两段区间都分别复制到一个数组内,根据位置对照的关系,删去原本的值,添加新的值即可。知道了上面两个的方法,操作 6 就格外简单了,将给定的区间存到一个数组内,接着根据位置关系插入新的值,删去之前的值即可。
用 0/1 分别表示数字,没有出现或出现了,用珂朵莉树维护连续出现的数字和连续没有出现的数字,即连续的 1 和连续的 $0$,那么操作 1 和 2 只需要根据要求反转 0/1 即可,而操作 3 就是将整个序列都进行了 0/1 反转,这样这道题目也变成了大水题。
总结:
上面题目的题单
区间操作题目是一种在 OI 中十分常见的题目,你们会发现,用线段树做,就是动态开点,建图优化,可持久化线段树,可在分块珂朵莉树中,不过是模板题的转化,而且这两种算法不一定只能用在区间操作题中,更是可以成为你做题中的一种十分通用的概念,
就先将这些题目了,欢迎各位巨佬的观看,希望能给大家带来帮助。