姓名: 陈言哲
赛道: 基础组
类型: 基础算法
【基础算法大总结】
关键词: 搜索、栈和队列和亿点点知识点
1.结构体
C++中的结构体可以理解成把几个相同或不同的数据组合在一起。
例如:
struct Node{
string name;
int age;
};
上面的Node结构体包含一个string类型的名字,以及一个int类型年龄。
但最让人无语的是,它的后面要加上一个" ; ",幸好Dev-C++会自动补全,不然又会祸害许多记性不好的人。
调用结构体如下:
Node p;
cin>>p.name>>p.age;
cout<<p.name<<p.age;
可以定义一个Node类型的p,在它的后面加个" . ",就可以调用了。
结构体中也可以定义函数:
struct Node{
string name;
int age;
void sayhello(){
cout<<"I am "<<name<<".\n";
cout<<"I am "<<age<<" years old.";
}
};
int main(){
Node p;
cin>>p.name>>p.age;
p.sayhello();
return 0;
}
如果输入"Bob"和"13"的话,它会输出:
2.排序
排序有很多,例如:选择排序,冒泡排序,插入排序······
但真正要用的时候,只需要一个sort就可以了,比如要给a数组从小到大排序:
int a[1005];
a[0]=3;
a[1]=8;
a[2]=2;
a[3]=6;
a[4]=5;
a[5]=10;
sort(a,a+6);
再从0开始输出就是2,3,5,6,8,10,这样一个有序的数列。
sort也有坑人的时候:
比如家族迁徙那题,单纯用sort是WA,用stable_sort才AC啊!!!

3.二进制与位运算
我们常常说的十进制,其实就是数到10,进一位。
二进制也一样,就是数到2,进一位,这就是它只有0和1的原因。
程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如,and运算本来是一个逻辑运算符,但整数与整数之间也可以进行and运算。举个例子,6的二进制是110,11的二进制是1011,那么6 and 11的结果就是2,它是二进制对应位进行逻辑运算的结果(0表示False,1表示True,空位都当0处理)。
实在看不明白的话去百度搜位运算。
按位与(&)
按位或(|)
按位异或(^)
按位取反(~)
左移(<<)
右移(>>)
明白了吗???
4.递推和递归
递推就是按照一定的规律来计算序列中的每个项,通过计算前面的一些项来得出序列中的指定项的值。实际上就是把一个复杂的计算过程转化成一些简单的过程,然后反复,直到推出了结果。递推利用了计算机速度快而且不知疲倦的机器特点。

简单来说就是找规律。
比如斐波那契数列,就可以用递推:
#include<bits/stdc++.h>
using namespace std;
int a[10005];
int main(){
int n;
cin>>n;
a[0]=1;
a[1]=1;
for(int i=2;i<=n;i++){
a[i]=a[i-1]+a[i-2];
}
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
return 0;
}
递归算法在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。递归式方法可以被用于解决很多的计算机科学问题,因此它是计算机科学中十分重要的一个概念。
递归和递推的基础思想是一样的,但递归用的是函数,而且在函数里调用函数(就是找到符合判断条件才返回):
这次是求斐波那契数列的第n项
#include<bits/stdc++.h>
using namespace std;
int f(int n){
if(n==1||n==2) return 1;
return f(n-2)+f(n-1);
}
int main(){
int n;
cin>>n;
cout<<f(n);
return 0;
}
有很多算法都用到了递归,比如分治算法,深度优先搜索dfs,之后会介绍到。
5.分治
分治可以用这张图来理解
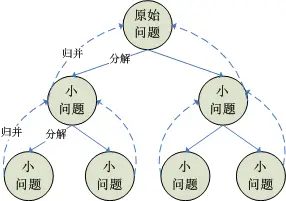
分治,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
再通俗一点就是把一片领土分解,分解为若干块小部分,然后一块块地占领征服,被分解的可以是不同的政治派别或是其他什么,然后让他们彼此异化。
分治算法具有以下的特点:
- 问题的规模缩小到一定的规模就可以较容易地解决。
- 问题可以分解为若干个规模较小的模式相同的子问题,即该问题具有最优子结构性质。
- 合并问题分解出的子问题的解可以得到问题的解。
- 问题所分解出的各个子问题之间是独立的,即子问题之间不存在公共的子问题。
分治法的精髓:
- 分–将问题分解为规模更小的子问题;
- 治–将这些规模更小的子问题逐个击破;
- 合–将已解决的子问题合并,最终得出“母”问题的解;
相当于递归,其实分治就是在函数里多调用几次自己。
6.二分查找
二分查找主要用到了三个指针:一个左指针,一个右指针,以及一个中间指针。
假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
模板:
//如果答案在mid处或在mid的左侧
int l=1;
int r=n;
while(l<r){
int mid=(l+r)/2;
if(/*条件*/){
r=mid;
}
else{
l=mid+1;
}
}
//如果答案在mid处或在mid的右侧
int l=1;
int r=n;
while(l<r){
int mid=(l+r)/2;
if(/*条件*/){
l=mid;
}
else{
r=mid-1;
}
}
7.栈和队列
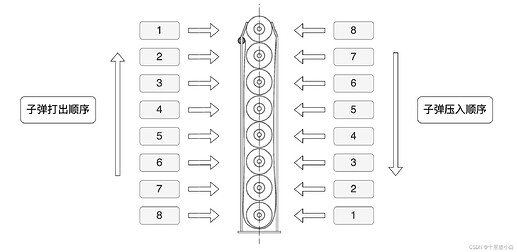
栈(stack)又称堆栈,是一种只能从头插入或删除数据的特殊线性表,具有先进后出的特点。
就比如枪压子弹:
栈通常有入栈(push),出栈(pop),取栈顶元素(top)以及判断栈是否为空(empty)四种用法。
例如:
stack<int> st;//声明一个栈
st.push(1);//把1入栈
cout<<st.top();//输出栈顶元素
st.pop();//删除栈顶元素
if(st.empty()){//判断栈是否为空
}
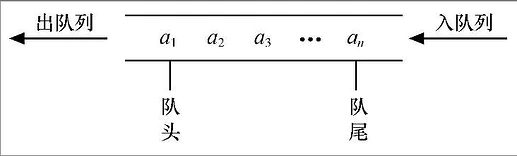
队列(queue)和栈一样,也是一种特殊线性表,但它只能从队头插入,队尾删除,具有先进先出的特点。
除了入队(push),出队(pop),取队头元素(front),判断队列是否为空(empty),队列还能取队尾元素(back)。
queue<int> qu;//声明一个队列
qu.push(1);//把1入队
cout<<qu.front();//输出队头元素
cout<<qu.back();//输出队尾元素
qu.pop();//删除队头元素
if(qu.empty()){//判断队列是否为空
}
8.搜索
深度优先搜索:
depth first search,简称dfs,
主要还是 不撞南墙不回头 递归,
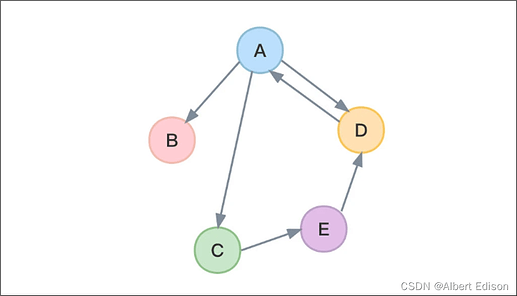
深度优先搜索属于图算法的一种,其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次.
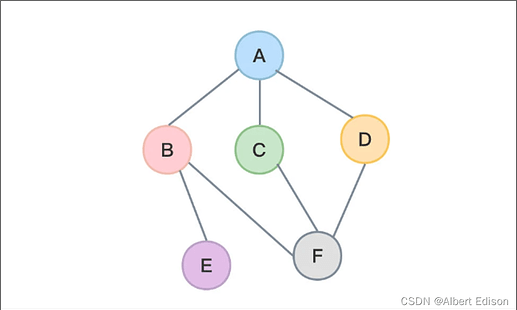
举例说明之:下图是一个无向图,如果我们从A点发起深度优先搜索(以下的访问次序并不是唯一的,第二个点既可以是B也可以是C,D),则我们可能得到如下的一个访问过程:A->B->E(没有路了!回溯到A)->C->F->H->G->D(没有路,最终回溯到A,A也没有未访问的相邻节点,本次搜索结束)
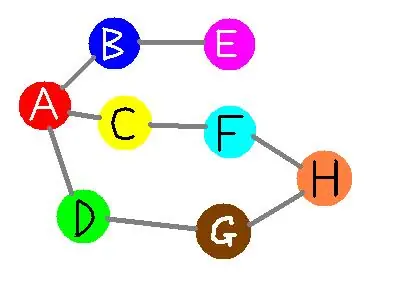
主要的结构如下:
void dfs(_____){
if(______){//如果____,就返回
return;
}
for(______){ //循环
if(______){//如果____,继续dfs
dfs(_____);
}
}
}
十分简洁,不要介意
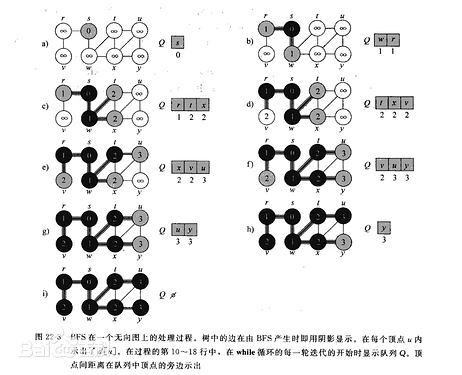
广度优先搜索
breadth first search,简称bfs
广度优先搜索并不使用经验法则算法。从算法的观点,所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。
比dfs长亿一点:
int dx[]={______};//行移动的方向
int dy[]={______};//列移动的方向
int n,m,stx,sty,enx,eny;//矩阵的长和宽,起点的横坐标和纵坐标,终点的横坐标和纵坐标
int vis[105][105];//访问数组
char mapn[105][105];//地图
struct Node{
int _____;//横坐标和纵坐标,以及一些时间等信息
};
void bfs(int x,int y,int time){
memset(vis,0,sizeof(vis));//初始化访问数组
vis[x][y]=1;//设起点为访问过的
queue<Node> qu;//定义一个Node类型的队列qu
qu.push({x,y,time});//把坐标等入队
while(!qu.empty()){//如果qu不为空
Node now=qu.front();//定义一个now取出qu的首位
qu.pop();//去除qu的首位
if(now.x==enx&&now.y==eny){//如果到终点了
cout<<now.time;//输出时间
return;//返回
}
for(int i=0;i<__;i++){//有几个方向就写几个
int now_x=now.x+dx[i];
int now_y=now.y+dy[i];
//now_x和now_y是现在的坐标
int now_time=now.time+1;//now_time是现在的时间
if(now_x<1||now_y<1||
now_x>n||now_y>m||
vis[now_x][now_y]==1){//如果越界了或者已经访问过了
continue;//跳过
}
vis[now_x][now_y]=1;//设置为访问过了
qu.push({now_x,now_y,now_time});//入队
}
}
}
9.树和图
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分
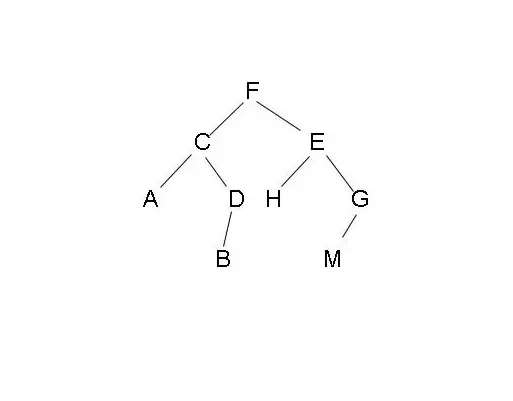
相关术语
①节点:包含一个数据元素及若干指向子树分支的信息。
②节点的度:一个节点拥有子树的数目称为节点的度。
③叶子节点:也称为终端节点,没有子树的节点或者度为零的节点。
④分支节点:也称为非终端节点,度不为零的节点称为非终端节点。
⑤树的度:树中所有节点的度的最大值。
⑥节点的层次:从根节点开始,假设根节点为第1层,根节点的子节点为第2层,依此类推,如果某一个节
点位于第L层,则其子节点位于第L+1层。
⑦树的深度:也称为树的高度,树中所有节点的层次最大值称为树的深度。
⑧有序树:如果树中各棵子树的次序是有先后次序,则称该树为有序树。
⑨无序树:如果树中各棵子树的次序没有先后次序,则称该树为无序树。
⑩森林:由m(m≥0)棵互不相交的树构成一片森林。如果把一棵非空的树的根节点删除,则该树就变成了一片森林,森林中的树由原来根节点的各棵子树构成。
有向图、无向图
如果给图的每条边规定一个方向,那么得到的图称为有向图。在有向图中,与一个节点相关联的边有出边和入边之分。相反,边没有方向的图称为无向图。
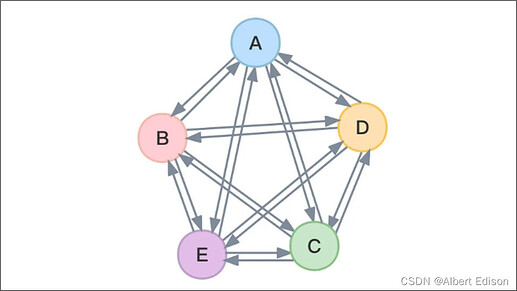
有向图:
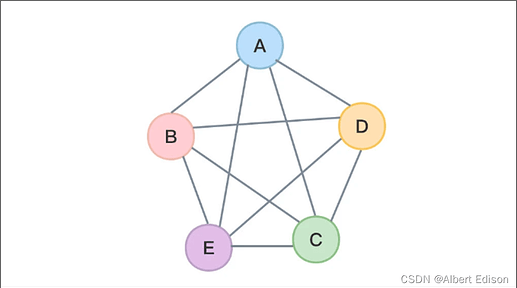
无向图:
有向完全图:
无向完全图:
单图
一个图如果任意两顶点之间只有一条边(在有向图中为两顶点之间每个方向只有一条边);边集中不含环,则称为单图。
邻接表,存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。
对于无向图来说,使用邻接表进行存储也会出现数据冗余,表头结点A所指链表中存在一个指向C的表结点的同时,表头结点C所指链表也会存在一个指向A的表结点。
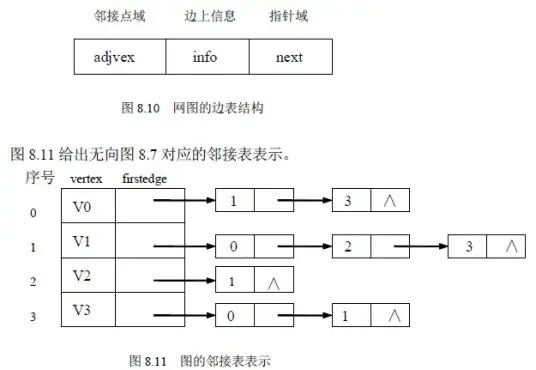
邻接矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵。设G=(V,E)是一个图,其中V={v1,v2,…,vn} 。G的邻接矩阵是一个具有下列性质的n阶方阵:
①对无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零(在此仅讨论无向简单图),副对角线不一定为0,有向图则不一定如此。
②在无向图中,任一顶点i的度为第i列(或第i行)所有非零元素的个数,在有向图中顶点i的出度为第i行所有非零元素的个数,而入度为第i列所有非零元素的个数。
③用邻接矩阵法表示图共需要n^2个空间,由于无向图的邻接矩阵一定具有对称关系,所以扣除对角线为零外,仅需要存储上三角形或下三角形的数据即可,因此仅需要n(n-1)/2个空间。
10.01背包
动态规划(Dynamic Programming,DP),利用一个表记录所有以及求解过的子问题的答案,只要一个子问题被求解过,就将其答案保存起来,无论以后的计算是否会用到。
01背包是在M件物品取出若干件放在空间为W的背包里,每件物品的体积为W1,W2至Wn,与之相对应的价值为P1,P2至Pn。01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品,每种物品有且只有一个,并且有权值和体积两个属性。在01背包问题中,因为每种物品只有一个,对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中,则不需要处理。如果选择将其放入背包中,由于不清楚之前放入的物品占据了多大的空间,需要枚举将这个物品放入背包后可能占据背包空间的所有情况。
代码举例:
#include<bits/stdc++.h>
using namespace std;
int t,m;
int dp[100005],w[100005],v[100005];//dp[i][j]用来记录第i件物品在背包容量为j是的最大价值
int main(){
cin>>t>>m;
for(int i=1;i<=m;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=m;i++){//遍历所有背包
for(int j=t;j>=0;j--){//遍历背包容量
//装得下 不装 装
if(j>=w[i]) dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
//装不下
else dp[j]=dp[j];
}
}
cout<<dp[t];
return 0;
}
看到这了,你就点个赞吧!!!!!