姓名: 钱瑞
赛道: 基础组
类型: 算法知识的总结
【基础算法大总结】
关键词: 算法总结,递归,递推,排序,dfs,bfs
笔记
结构体
结构体非常简单,其实就是自己新建的一种数据类型,下面是结构体的模板:
struct Node{
int x;
int y;
//其他的变量
//……(自己需要)
}
———————————————————————————————————————
排序
选择排序
选择排序非常简单,其实就是选出当前数组中最大的数并且和他的应当的位置的数进行交换
下面是选择排序的模板(升序):
for(int i=1;i<n;i++)
{
int m=i;
for(int j=i+1;j<=n;j++)
{
if(a[j]<a[m]) ________;//将m替换为j
}
if(a[i]>a[m])________;//交换
}
如果需要降序排序的话,只需要改动其中的一小部分就行了。
冒泡排序
冒泡排序的核心思想就是一个数和他的旁边的数比较,如果大于或小于(主要看是需要升序还是降序)就进行swap交换的操作来得到一个升序或降序的序列
下面是模板代码(升序):
for(int i=1;i<=a;i++){
for(int j=1;j<=a;j++){
if(sum[j-1]>sum[j]){
swap(sum[j-1],sum[j]);
}
}
}
难道这就是最优解了吗?
不!
还有更好的!!!因为我们在进行冒泡排序是有一部分数已经排列好了,再次进行判断会有冗余,我们需要将内层循环内将j赋值成i,就可以更快了,下面是优化后的代码:
冒泡排序优化代码:
for(int i=1;i<=a;i++){
for(int j=i;j<=a;j++){//需要修改的就是此处的j
if(sum[j-1]>sum[j]){
swap(sum[j-1],sum[j]);
}
}
}
插入排序
插入排序其实也非常简单,其实插入排序基本思想是每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。
下面是插入排序的核心代码:
for(int i=2;i<=n;i++){
cin>>a[i];
for(int j=i;j>=2;j--){
if(________){//a[j]<a[i-1]时
_________;//交换两者位置
}else{
break;
}
}
}
桶排序
桶排序别名计数排序,其运作的核心原理类似于将待整理的东西放入桶内,在放入桶内后这里的值需要累加。
下面是桶排序的核心代码(升序):
int sum,sum1;
cin>>sum;
for(int i=1;i<=sum;i++){
cin>>sum1;
__________;//累加
}
for(int i=1;i<=sum;i++){
for(int j=1;j<=a[i];j++){
__________;//输出
}
}
其实我们还可以利用桶排序制作去重排序,只需要输出改动内部的循环,判断这个桶里有没有存放数,下面是示例代码(升序):
for(int i=1;i<=n;i++){
cin>>b;
a[b]++;
}
for(int i=1;i<=100000;i++){
if(a[i]>0){//需要改动的地方就在这里
cout<<i<<" ";
}
}
sort排序
sort排序是一种快速排序,可以帮助我们只需要一行代码就写出排序,可谓是非常方便吖,(原理是什么,目前我这只小up还不知道,感兴趣的可以去搜搜)
使用方法(升序):
int a[10005]={……………………};//数组里有数据
sort(a+1,a+n+1);//其中第一个是起始位置,第二个是结束为止(后面还有一个cmp,不写默认升序)
如果我们想要获得一个降序排序的话,我们需要使用一个cmp(自定义排序方法)来辅助我们排序,下面是使用方法:
使用方法(降序):
bool cmp(int a,int b){
return a>b;
}
int a[10005];
sort(a+1,a+n+1,cmp);
这样你就可以获得一个降序排序了。
结构体排序
其实结构体排序不太好讲,所以我这里简单讲讲(深入讲的话又要占一期内容了),结构体排序需要使用我们的cmp(自定义排序方法),下面是模板代码:
struct Node{
int x;
int y;
}
bool cmp(Node a,Node b){
if(a.x!=b.x){
return a.x>b.x;
}else{
return a.y>b.y;
}
}
sort(a+1,a+n+1,cmp);
这点代码使用cmp,配合sort函数完成了按照x的升序排序,如果x相等时,按照y的升序排列,比我们手写swap要强多了!!!
stable_sort
stable_sort函数是是sort函数的分支,是sort的另一个版本,函数的参数一模一样的,下面是示范代码:
int a[10005];
stable_sort(a+1,a+n+1,____);//后面空出来的格子可以填cmp
部分总结:
排序的性质
时间复杂度
冒泡排序,选择排序,sort(),插入排序,stable_sort(),结构体排序,一般都是O(n²)(相对与桶排序比较耗时,但是省空间)
桶排序:O(n)(相比于其他排序,省时间但是费空间,请不要将数组开太大)
稳定度
选择排序,插入排序,sort(),插入排序不稳定(元素前后位置改变)
冒泡排序,stable_sort()稳定(元素前后位置不改变)
———————————————————————————————————————
贪心
贪心算法的核心思想是以局部最优解来达到全局最优解,但是这种思维方式并不是在所有地都适用
例如:小明买了一个玩具,需要支付店家98元,问:至少需要用多少张纸币(小明有的纸币数量足以支付(不存在纸币不够用的情况)):
其实这题的思路就是上面的贪心算法,为了是支付的纸币数量最少,我们需要优先支付小于当前剩余需要支付的钱数的最大面额的纸币,按照以上思路,我们可以得出最小的值:
98=50+20+20+5+2+1(算上二元的纸币)
也就是最少需要6张纸币。
为了让大家举一反三,我也是直接出一题好吧!!!(很简单的)
1. NOIP2007-J-2-纪念品分组
题目ID:1485必做题100分
最新提交:
Accepted
100 分
历史最高:
Accepted
100 分
时间限制: 1000ms
空间限制: 262144kB
题目描述
题解
这题的思路其实就是最大的和最小的结合,如果最大+最小<=限制的值,那么直接把最大的和最小的放在一起,否则,如果最大的<=限制的值,那么我们直接将最大的分成一组,如果还是大于限制的值,那么,我们将最小的那个分为一组,怎么样,我相信懂得都懂,也是
just so so,so easy and too water!!哈哈哈
然后就是核心代码(带注释)
while(L<=R){
if(L!=R){
if(arr[L]+arr[R]<=k){
cnt++;
_______;//累加L
_______;//累减R
//其实他俩的意思就是把他俩分在了一组里
}else if(arr[R]<=k){
cnt++;
_______;//否则就你直接将大的分为一组
}else{
cnt++;
L++;
}
}else{
L++;
cnt++;
}
}
cout<<cnt;
问:这道题的贪心策略是什么?
_________________________。
第一个答对的人送解决方案
———————————————————————————————————————
枚举
枚举没什麽好说的核心思路就是用暴力拆解问题,直到得到正确答案。
模拟
模拟也没有什么好说的,就是照着题目给你的去做就可以了。
高精度
加减法
高精度加减法的核心思路就是模拟我们在列竖式的过程,满十进一,不够减就借位
乘除法
高精度乘除法也是一样,也是在模拟我们在列竖式的过程,但是,需要注意的是:
(黑色背景的可能看不见图片)
如果两个数位相乘(设个位为0位),则两位相乘所得到的乘积要放到数组的第i+j位上。
二进制与位运算:
二进制不讲了,应该都会。
重点是位运算
>>//右移一位,相当于*2
<<//左移一位,相当于/2
|//或运算
&//与运算
这就是位运算的基本运算符号。
———————————————————————————————————————
递推
递推是运用递推关系式来推出最后答案的一种算法,其实还是比较简单的,下面是一道例题(实在是没啥好讲,就直接例题实战,相信大家递推一定学过)
题目
我们分析一下这道题,因为每次上楼梯都有上一节台阶或两级台阶,于是我们从1开始找上楼梯的总方法数
//1:1 1种方案
//2:11 2种方案
//3:111 12 21 3种方案
//4:1111 112 121 211 22 5种方案
//5:11111 1112 1121 1211 2111 122 212 221 8种方案
相信很多小伙伴已经看出来他们的关系了,啊对,a[i]=a[i-1]+a[i-2],就是此题的递推关系式了,下面是代码:
void Node(int n,long long a[]){
for(int i=3;i<=n;i++){
_________;//递推关系式
}
__________;//输出第n个数
}
这就是这题的核心代码。
———————————————————————————————————————
递归
递归的本质是在函数本身里面调用本身,以此来算出答案,下面直接给你们出一道题,(没事,真的很简单的)
分治
分治在本质上也是一种递归,但是他的核心思路和普通递归不一样,而是把大的问题拆分成更小的问题来进行更快地运算
二分查找
二分查找是一种快速的查找方式,但是这种查找方式仅限于有序的序列中,才可以使用,所以一般要使用sort()函数进行排序
栈和队列
栈是一种不同与数组的存储方式,栈先进后出,就是先进去的元素后面出来,就像你们家中的垃圾桶一样 队列也是一种不同与数组的存储方式,队列先进先出,就像排队一样,先排队的人,先能排到的道理一样。
———————————————————————————————————————
树和二叉树
笔记
节点的度
节点拥有的子树个数或者分支个数
树的度
树拥有的最大的节点个数
根的度
在整个树最上端的节点拥有的分支个数
根节点
一棵树至少有一个节点,这个节点就是根节点
叶子节点
又叫做终端节点,指度为0的节点
非终端节点
又叫分支节点,指度不为0的节点,都是非终端节点,除了根节点之外的非终端节点,也叫做内部节点。
父节点,双亲节点
称上端节点是下端节点的父节点。
孩子节点
称下端节点为上端节点的子节点。
兄弟节点
称同一个父节点的多个子节点为兄弟节点。
祖先节点
又称从根节点到某个子节点所经过的所有节点称为这个点的祖先
子孙节点
称以某个节点为根的子树中,任意节点都是该节点的子孙
以上就是二叉树专用名词的解释了
———————————————————————————————————————
dfs类问题
搜索与回溯
这一篇重要的是:回溯需要清除访问数组留下的痕迹,千万别忘了
全排列应用
全排列也是需要使用访问数组的,因为这其实就是选完了不能再选的问题,回溯也需要清除访问数组留下的痕迹
迷宫类dfs
其实和上面的类似,(我都不想讲了,累死了),纯粹就是从一维变成二维罢了,需要一个二位的访问数组来进行回溯,并且需要向量进行移动。
下面是一个向量:
int dx[]={0,0,1,-1};
int dy[]={-1,1,0,0};
在这个向量中模拟了迷宫中上下左右的移动方法。
棋盘类dfs
和迷宫类基本一模一样,只不过移动方式可能不太一样,下面是一个象棋“马”的向量
dx[]={2,2,1,1,-1,-1,-2,-2};
dy[]={1,-1,2,-2,2,-2,1,-1};
搜索设计
《教你如何设计一个搜索》,其实真的很难,建议去看我的帖子,但是真的没啥好讲的
bfs部分
bfs不是一种递归,所以,他不是一种递归,他的速度也是dfs更快的,他也需要一个向量,用在不同的情景当中进行移动位置,dfs的解决范围一般比dfs大,因为他比较快,可以更快捷的解决,并且bfs第一次找到的,一定是最优方案,不像dfs一样一边一遍的试错拆能得出答案。
##树和二叉树
树是一种单对多的数据结构,二叉树是树的一部分,二叉树的基本特征是子树数量不超过2个。
图
不是,为什么可恶的图又来骚扰我们这些三好市民了吖,我也是真的服了吖,所以,为了让我们的童靴不再担心我们可恶的图,我也是直接出了一个知识点来帮助大家吊打可恶的图!!!
有向图
有向图,顾~~~名思议,就是带有方向箭头的图,即每条边都有方向,在有向图中,通常将边称为弧,含箭头的一端称为弧头,另外一端称为弧尾,记作
<vi,vj>
他表示从顶点vi到顶点vj有一条边
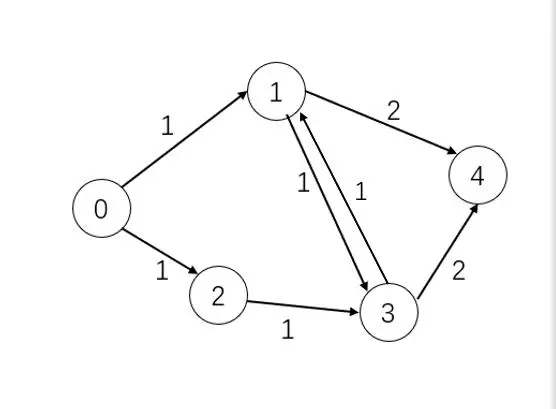 《有向图》
《有向图》
你以为这就完了???不远远还没有
顶点的度
顶点的度以顶点为一个端点的边的数目
对于无向图(就是没有箭头、方向的图)顶点的边数为度,度数之和是顶点边数的两倍,如下图所示,v3的度是4:
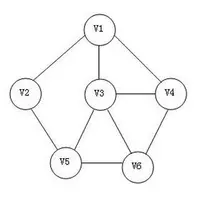
对于有向图,入度是以顶点为终点,出度相反,有向图的全部顶点入度之和等于出度之和,且等于边数。如上面出现的图所示:

(注意:入度和出度是针对于有向图来说的)
还没完!!!
无向完全图
在无向图中,如果任意两个顶点之间都存在边,则改图被视为无向完全图,含有n个顶点的无向完全图有n(n-1)/2条边
有向完全图
如果任意两个顶点之间都存在互为相反的两条边,则称该图为有向完全图,含有n个顶点的完全图有**n(n-1)**条边。
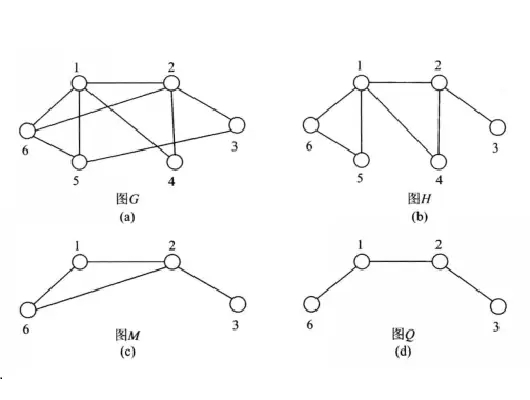
子图
假设有两个图G={V,{E}}和G’={V’,{E’}},如果V’是V的子集,且E’是E的子集则称G’为G的子图,如图H,图M,图Q都是图G的子图。
连通图
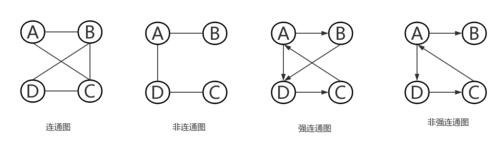
在无向图中,如果从顶点v到顶点v’有路径,则称v和v’是连通的。如果对于途中任意两个点vi,vj都是联通的,则称这个图是连通图!!!
以上可就是这次的全部内容了
(狂干4小时,给作者点个赞吧,求求了(胡桃的祈求))
懂?
- 会了
- 废了
- 吖?
点个赞吧,求求了!!!
版权为是一只原癖的linan04103所有,请勿侵权!!!