提高模考7.30 T4《柱状图》题解

经验分享区
311

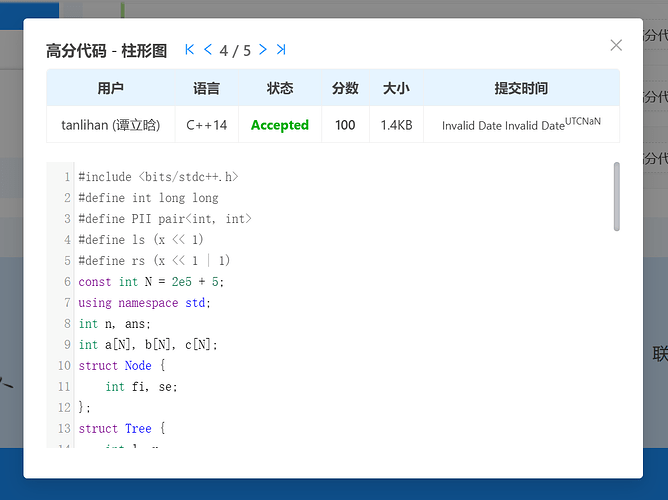
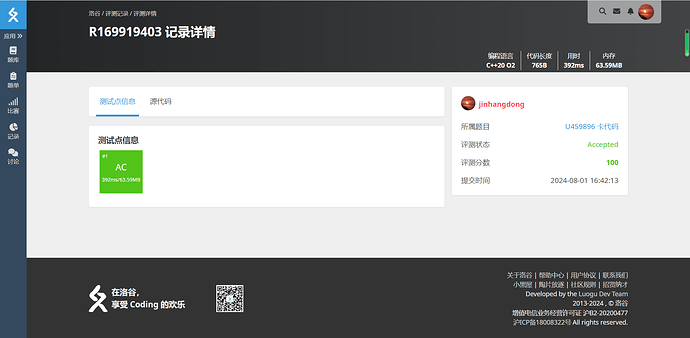
首先，分析的是平均复杂度，其次，平均复杂度也是在乱分析/cf

1 个赞
313

这么说我直接认为所有树的树高都是logn好了，反正平均就是这样

2 个赞
315

是的，一般来说最坏复杂度才有正解的参考意义

2 个赞
318

要不你给出一组数据。
你可以试一试，卡掉几乎不可能

2 个赞
322

可这是你自己说的非正解

1 个赞
323

广东 D 类金牌爷说过，这种问题类似字符串哈希只要算期望就行。

这个的真正问题是他平均复杂度的分析非常不严谨。

1 个赞
333

但是他就用那个当作不TLE的依据不应该很值得抨击吗。

1 个赞
334

我并不否认其作为题解的价值但是它要是作为“是否正确”的依据是毫无道理的。

1 个赞
335

我还是认为，这种思路是值得我们学习的，首先你还没卡掉，其次你卡掉也是故意卡掉的，还是一种很好的思路。

P.S. 我只是提供一种估算方法，并不是严谨证明，这个我做不了，但是你们（目前还）卡不了。并且，我已经知道我的并不严谨，因此请看前面，我说过勿喷。

建议关贴。

2 个赞
338

image
image1053×787 51.2 KB

已卡掉。连接

1 个赞
339

数据发一下

1 个赞
340

还是一种很好的思路。

我承认能过题我也卡不掉，但是很好的思路的前提难道不是正确吗。

1 个赞
342

已添加到那道题的附件下面

1 个赞
345

image
image1920×943 102 KB

卡了？？

1 个赞
346

把O2关了

1 个赞
347

不行，试试这份

#include<bits/stdc++.h>
#define ll long long
#define N 200005
using namespace std;
int n,lg[N];
int dp_a[N][25],dp_b[N][25];
ll ans=0;
int query_a(int l,int r){
    int k=lg[r-l+1];
    return min(dp_a[l][k],dp_a[r-(1<<k)+1][k]);
}
int query_b(int l,int r){
    int k=lg[r-l+1];
    return min(dp_b[l][k],dp_b[r-(1<<k)+1][k]);
}
vector<int> v;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
		scanf("%d%d",&dp_a[i][0],&dp_b[i][0]);
		v.push_back(i);
    }
    for(int i=2;i<=n;i++){
        lg[i]=lg[i>>1]+1;
    }
    for(int i=1;i<21;i++){
		for(int j=1;j+(1<<i)-1<=n;j++){
			dp_a[j][i]=min(dp_a[j][i-1],dp_a[j+(1<<i-1)][i-1]);
			dp_b[j][i]=min(dp_b[j][i-1],dp_b[j+(1<<i-1)][i-1]);
		}
    }
    random_shuffle(v.begin(),v.end());
    for(auto i:v){
    	for(ll j=i;j<=n;j++){
    		ll x=1ll*query_a(i,j)*query_b(i,j);
    		ans=max(ans,x*(j-i+1));
    		j=(ans/x)+i-1;
		} 
	}
	cout<<ans;
    return 0;
}
1 个赞
348

那题是2.5秒

1 个赞
350

信友队时限是1s，另外，这也说明这种代码是可以卡掉的（）

1 个赞
352

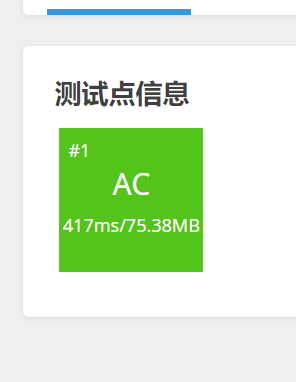
image

不对啊，卡不掉

1 个赞
353

@刘恩印

#include<bits/stdc++.h>
#define ll long long
#define N 200005
using namespace std;
int n,lg[N];
int dp_a[N][25],dp_b[N][25];
ll ans=0;
int query_a(int l,int r){
    int k=lg[r-l+1];
    return min(dp_a[l][k],dp_a[r-(1<<k)+1][k]);
}
int query_b(int l,int r){
    int k=lg[r-l+1];
    return min(dp_b[l][k],dp_b[r-(1<<k)+1][k]);
}
vector<int> v;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
		scanf("%d%d",&dp_a[i][0],&dp_b[i][0]);
		v.push_back(i);
    }
    for(int i=2;i<=n;i++){
        lg[i]=lg[i>>1]+1;
    }
    for(int i=1;i<21;i++){
		for(int j=1;j+(1<<i)-1<=n;j++){
			dp_a[j][i]=min(dp_a[j][i-1],dp_a[j+(1<<i-1)][i-1]);
			dp_b[j][i]=min(dp_b[j][i-1],dp_b[j+(1<<i-1)][i-1]);
		}
    }
    random_shuffle(v.begin(),v.end());
    for(auto i:v){
    	for(ll j=i;j<=n;j++){
    		ll x=1ll*query_a(i,j)*query_b(i,j);
    		ans=max(ans,x*(j-i+1));
    		j=(ans/x)+i-1;
		} 
	}
	cout<<ans;
    return 0;
}
1 个赞